鎖を引き上げる力
鎖の運動には質点や剛体の運動にはない難しさがあるが、同時に、鎖はニュートンビーズのような面白い振る舞いをする。昔、教養部の物理の授業で使用していた上下2分冊からなる教科書(金原寿郎編:裳華房基礎物理学1963年)の上巻P.101 に、次のような興味深い鎖の問題が載っていた。
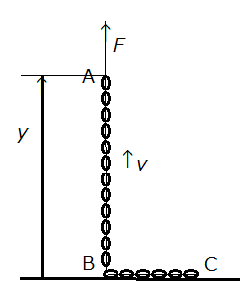
[問題] 図1のように、線密度ρの鎖の一端、A点を一定の速さv(v>0)で引き上げるときの力Fを求めよ。ただし、鎖のBC部分は水平に描かれているが机の上の一ヶ所にひとかたまりに置かれているとする。
[通常の解法] AB部分の長さをyとすると、その質量はρy、それが速度vを持つので、運動量Pは、P=ρyv、運動方程式は、dP/dt=F−ρgy・・・(1)、よつて、 F=ρgy+ρv2 ・・・(2)となる。
この問題は、一見、簡単なようでも、実際には大学生でも戸惑う。それを、敢えて高校生に解かせたらどう解くか、高校生に戻ったつもりで考えてみた。
[高校生の解法] 大学生には当然なことでも、高校生にとってはそうはいかない。(1)の運動方程式は、[運動量の時間微分=力]・・・(3)であるが、高校の教科書では、運動方程式は、 [質量×加速度=力]・・・(4)であり、質量が保存している場合しか適用できない。高校生が(4)を適用して鎖の問題を解くには、鎖のAB部分だけでなく、BC部分も含めた鎖全体に対する運動方程式を考えなければならない。Lを鎖の全長とすると、鎖の質量はρLである。AB部分の重心の高さはy/2、静止しているBC部分長さはL-yであり、その高さは0だから、鎖全体の重心の高さyGは、 yG =y2/2L・・・(5)となる。yの時間微分はvであるから、(5)式を2回時間微分すると、重心yGが上昇する加速度αは、α=v2/Lとなる。運動方程式から、質量(ρL)と加速度(v2/L)との積が鎖に働く力(F-ρgy)に等しく、 F=ρgy+ρv2 が導かれ、通常の解法で導かれる(2)式と一致する。
仕事とエネルギー
力Fを求めるだけなら上記のように高校生にも何とか解けそうだが、さらに力がした仕事となると、さらに難しくなろう。力Fとその作用点Aの微小変位dyとの積は、(2)より、Fdy=ρgydy+ρv2dyとなるが、これは、Fが鎖にした仕事だから、熱エネルギーまで含めた鎖のエネルギーの増し分であり、鎖の力学的エネルギーだけの増し分ではない。それでは、次に鎖の力学的エネルギーを求めてみよう。
[準静的過程と定常過程] A点を任意の高さhまで引き上げるために必要な仕事を考えよう。ただし、h<Lとする。まず、引き上げる速さvが限りなく0に近い場合、引き上げる力をF0とすると、(2)式からF0=ρgyとなり、F0を、yで、y=0からy=hまで積分すると、準静的に引き上げたときの仕事W0は、W0=ρgh2/2となり、鎖の位置エネルギーに等しくなる。それに対し、有限な一定速度vでA点を高さhまで引き揚げたときの仕事は、(2)式をyで0からhまで積分して、 W=ρgh2/2+ρv2h・・・(6)となる。有限な速度で引き揚げると、仕事Wは、準静的に引き上げたときの位置エネルギーW0より、ρv2hだけ大きいが、これは長さhの鎖の重心の運動エネルギーに等しくはない。鎖のAB部分に働く力は、F−ρgyだが、それは(1)式より、ρv2であり、yによらず一定となる。A点を高さhだけ引き上げたとき、長さhの鎖は一定の上向きの力ρv2を受け、その重心がh/2だけ移動する。よつて重心運動のエネルギーは、ρv2h/2になり、鎖が得た力学的エネルギーEは、 E= ρgh2/2 + ρv2h/2・・・(7)となる。つまり、高さhだけ引き上げられると、(6)式と(7)式からW−E= ρv2h/2が失われている。
[ふたつの仕事] 高校物理の教科書の力学の箇所では、仕事を、[仕事=力と物体の移動距離の内積]・・・(8)と定義し、それに対し理化学辞典には、[仕事=力と作用点の変位との内積]・・・(9)とある。(8)式の力は物体に働く全ての力であり、物体の移動距離とは重心の変位である。(8)は(9)に含まれる仕事ではなく、また仕事の対象を質点に限定した仕事でもない。鎖は質点ではない、また、鎖は質点とは見做せない。(8)と(9)の違いは、仕事をしたとき、そのエネルギーが物体の重心運動のエネルギーになるか、それとも物体全体の熱エネルギーまで含めた全エネルギーになるかであり、どちらも物理にとって必要な仕事である。
[力学的エネルギーの損失] 鎖の運動において定常的に速さvで引き上げるとき、力学的エネルギーのρv2h/2が失われたのは、定常的に非弾性衝突が起きているからだが、何と何とが衝突しているのだろうか。鎖を引き上げる時、B点にやって来た鎖の粒は、常に静止した状態から、急に有限の速度vを持つので、非弾性衝突と同じになるが、それは次のように説明すると分かり易い。糸で結んだ物体1と物体2が、糸がたるんだ状態で摩擦のない台の上に静止しているとしよう。その状態から、物体2に速度を与えると、糸がたるんでいるので、最初は物体2だけ等速度運動するが、糸がピーンと張ると、そのあと、2つの物体は同じ速度を持つ。これは台の上に静止していた物体1に物体2が衝突し、衝突後、両者が一体となって運動する非弾性衝突と同じである。鎖は力学的エネルギーを熱として散逸させながら引き上げられている。鎖のA点をhだけ引き上げたときのエネルギー損失は ρv2h/2で、h=vtだから、単位時間当たり、ρv3/2の力学的エネルギーが熱に変化している。
ここまで理解した上で鎖の面白い運動について考えてみよう。鎖の噴水 につづく。

コメント