少年期に訪れる反抗期は麻疹のようなものだが、人より遅れての反抗期は少々厄介のようである。定年退職後に突如、反抗期?になったのか、学会に楯つく暇人と、物理教育学会会誌編集委員会との、互いに火花を散らし、口角泡飛ばしての論争も愈々正念場。コロナ禍のなか、どちらの応援かに関わらず、物理ファンの皆様を、火花も飛沫も浴びないよう、安全性を配慮してネットでの観戦にご招待したい!
動かない壁や床から受ける力のように、作用点の動かない力、抗力などの束縛力が、仕事をすると言えば、問答無用とばかりに、即「トンデモ説」のレッテルを貼られるのは、もとより承知の上だが、並進運動と回転運動とが絡んだ複合運動の場合、抗力のする仕事を否定して、二つの運動への力学的エネルギーの配分をどう説明するだろうか。
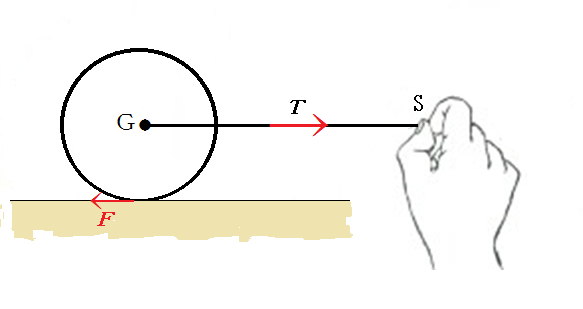
毎回お馴染みの円柱の転がり運動だが、図1のように、半径r、質量M、慣性モーメントIの円柱の重心Gに、質量の無視できる取っ手を付け、それを水平方向に外力Tを加え引っ張ったとき、円柱が机の上を滑らずに転がる運動を考えてみよう。このとき円柱に働く水平方向の外力は、Tと、机との接点において机から左向きに受ける水平抗力Fの二つだけである。円柱は滑らないので、Fは机から受ける静止摩擦力であり、その作用点は動かない。転がり運動は並進運動と重心のまわりの回転運動とからなる複合運動であるから、その運動方程式は、二つの運動の運動方程式が、抗力Fを介して結び付いた次のような連立方程式で表される。
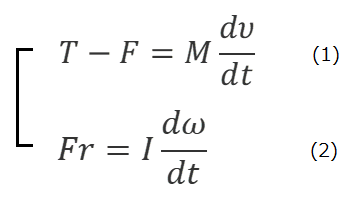
ここで、v およびωはそれぞれ、並進運動の速度および回転運動の角速度であり、円柱がすべらない場合には、v=rωなる条件が加わる。(1)式と(2)式かなる連立方程式が、図1に対する運動方程式であるためには、力Tが与えられたとき、これを解くことにより、円柱の転がり運動に関する次の①~⑥の全てが導かれなければならない。
①水平抗力Fの大きさ ②円柱の運動量 ③円柱の角運動量 ④円柱の並進運動のエネルギー ⑤円柱の回転運動のエネルギー ⑥円柱の全体運動のエネルギー
①については、円柱の場合、その中心軸のまわりの慣性モーメントはI=Mr2/2から、(1)と(2)式から、F=T/3となる。②については、連立方程式の片方の(1)式を時間tで積分すれば、左辺(T-F)の時間積分、つまり、力積が、円柱の運動量Mvの増し高⊿(Mv)に等しくなる。T=0であれば、Fも0になり、Mvは一定となり、運動量保存則が成り立つ。③についても(2)式を積分すれば、力積のモーメントが角運動量Iωの増し分に等しくなり、T=0の場合には、角運動量の保存則も成り立つ。
④と⑤のエネルギーについては、それぞれ、(1)および(2)の左辺の力および力のモーメントがする仕事を求めればよい。それには、(1)の両辺に重心の変位dxG=vdt を掛け、(2)の両辺に回転角の変化dθ=ωdtを掛け、数学を用いて、それぞれの右辺を変形すれば、連立方程式(1)(2)は、次のようになる。
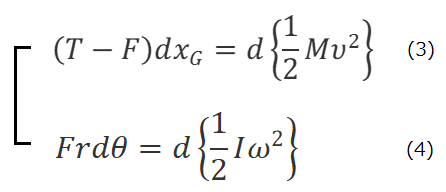
(3)式および(4)式の右辺は、それぞれ、並進運動および回転運動のエネルギーの増し分であるから左辺はそれぞれ並進運動および回転運動になされた仕事である。(3)と(4)式は、二つの運動が、それぞれのエネルギーを得るために、外部の動力源が円柱に及ぼす力Tが並進運動に仕事をし、水平抗力Fが並進運動に負の仕事をすると同時に回転運動に正の仕事をすることが分かる。(3)と(4)を加えると
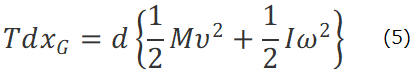
となる。(5)式は、外部の動力源がした仕事である左辺が、円柱の力学的エネルギーの増し分である右辺に等しいことを表しているが、それは仕事とエネルギーの内訳を表す(3)式と(4)式から導かれる。円柱の転がり運動に関する①~⑥の物理量はすべて(1)と(2)式から導かれることが分かる。運動方程式に基づいた極めて普通の説明と思えるが、以上の説明のどこが「トンデモ説」だろうか。
しかし、40年前にアメリカで発表された論文(今後これをPseudowork論文と呼ぶことにする):Am.J.Phys.Vol.51(1983)によれば、上記の説明は間違いだという。その理由は、仕事の正しい定義は力と力の作用点の変位との内積であり、(3)式の左辺は、作用点が動かない力Fを含むから仕事でなく、仕事に似て仕事でないpseudoworkだという。それなら、(4)式の左辺も同じ理由でpseudoworkになろう。しかし、上記論文は(4)式には触れず、(3)式の左辺をpseudowork、(5)式の左辺をrealworkとして議論をしている。議論の出発点を(1)と(2)からなる連立運動方程式ではなく、(3)式と(5)を選んだのでは、①~⑥のうち、⑥だけしか説明できない。つまり、Pseudowork論文は運動間のエネルギーのやり取りを説明できず、エネルギーのドンブリ勘定になっている。
Pseudowork論文の誤りは固定観念に囚われ、抗力は、その作用点が動かないので仕事をしないと決めつけている点にある。力学における仕事の正しい定義は、並進運動に対しては、力と物体の変位との内積(これを仕事Aと呼ぶことにする)であり、回転運動に対しては、力のモーメントと回転角の変位との積(これを仕事A’と呼ぶことにする)である。高校物理教科書も広辞苑もブルタニカ科学百科事典の記述も仕事Aである。仕事A’は仕事Aを回転運動に拡張した仕事である。
ただし、熱力学や物性を念頭に置いた理化学辞典では、仕事は力と作用点の変位との内積(これを仕事Bと呼ぶことにする)である。図1の転がり運動では、並進運動に対する仕事は仕事Aであり、回転運動に対する仕事は仕事A’であり、全体運動の転がり運動に対する仕事は、熱力学と同じく仕事Bであることが分かる。
仕事の定義は物理法則ではないが、物理法則に基づいて定義されなければならない。(3)式の左辺の仕事は、並進運動の運動運動方程式に基づいて定義された並進運動に対する仕事である。運動法則は抗力Fと外部の動力源から受ける外力Tとを区別していない。(3)式はその仕事が円柱の並進運動のエネルギーの増し分に等しいことを示し、同様に(4)式の左辺の仕事は、回転運動のエネルギー増分に等しく、回転に対する運動方程式に基づいて定義された仕事A’である。(3)と(4)式を加えて得られる(5)式の左辺の仕事は、外部の動力源が転がり運動にした仕事であるから、仕事Bである。どの仕事も物理法則に基づき、力学的に明確な意味のある仕事であり、pseudoworkなどが入り込む余地はない。抗力が仕事をする場合、必ず正と負の仕事が一対として現れるので、抗力が仕事をしても不都合なことは一切起こらない。
もし、(3)式と(4)式を導く前に、運動方程式(1)と(2)式からいきなり先にFを消去すると、
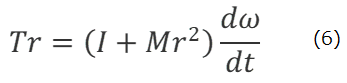
となり、(6)式からも(5)式を導くことができる。しかし、(6)式は、もはや、図1の転がり運動に対する運動方程式ではない。(6)式は、抗力Fを消去したため(1)と(2)式からなる転がり運動の連立方程式に含まれていた①~⑤の情報が失われている。(6)式から導かれるのは⑥の全体運動のエネルギーだけになる。
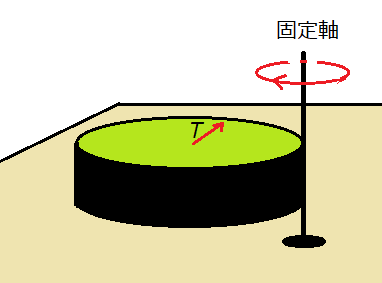
(6)式は、図1のような複合運動の運動方程式ではなく、抗力を消去したため、図2のように、回転軸が固定され、そのまわりの慣性モーメントが I+Mr2 の剛体に力のモーメントrTが働いて回転する場合の運動方程式と同じである。円柱と机との接点を固定し、そのまわりに円柱が回転しているから、そのときの慣性モーメントは I+Mr2 であり、(6)式の両辺にdθ=ωdtを掛けると、同じ(5)式が得られるが、(6)式は、複合運動ではなく、固定軸のまわりの回転の運動方程式であり、単一運動に対する運動方程式にすり替わっている。
複合運動も、運動全体に対する仕事は(5)式で表されるように仕事Bになるが、単一運動では、それ自身が全体運動であるから、仕事Aも仕事A’も仕事Bと同じになる。しかし転がり運動のような複合運動では仕事Aも仕事A’も仕事Bにはならない。図1のような複合運動は、特殊な運動ではない。図1では動力源が外部に存在しているが、動力源が内部に存在しているときは、その運動は全て複合運動である。
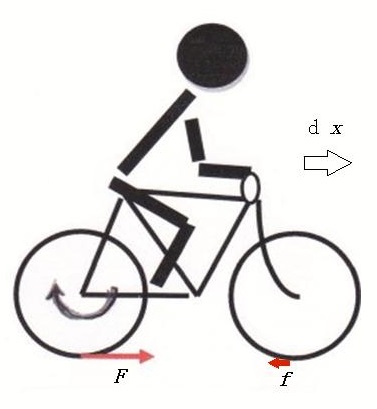
動力源が系内に存在する例として、図3のように、動力源が系の内部に存在する場合の複合運動をを考えてみよう。自転車に乗って加速するとき、人と自転車からなる系に働く水平方向の外力は、自転車の後輪に道路から進行方向に働く抗力Fと、前輪に後ろ向きに働く抗力fだけである。人を含めた自転車の並進運動に仕事をする力は、この二つの抗力以外に存在しない。
エネルギー源は人であり、人の筋力は内力だから系の並進運動に直接仕事をすることはできないが、後輪の回転運動に対しては、ペダルとチェーンを通して、後輪の回転運動に右回りの力のモーメントとして働き、回転運動に仕事をする。しかし、いくらペダルを踏んでも、抗力Fが働かなければ、後輪が回転するだけで、並進運動は加速されない。加速するには、抗力Fが後輪の回転運動に負の仕事をし、同時に並進運動に正の仕事をする。並進運動が加速されると、前輪に後ろ向きの抗力fが生じ、fは並進運動に負の仕事をし、前輪の回転運動に正の仕事をする。
高校の物理教科書は改訂に改定を重ね、多くの物理関係者が関わって出来上がった極めて完成度の高い教科書だと思う。もし、Pseudowork論文の主張が正しく、抗力のする仕事がトンデモ説なら、仕事として、仕事Aを採用している高校物理教科書も「トンデモ本」になろう。しかし、仕事Aはニュートンの運動法則に基づいて定義された正しい厳密な仕事の定義である。
物理教育学会が、頑迷なまでにPseudowork論文を信奉し、仕事Bを唯一の仕事として、高校物理教科書の仕事の記述を否定するなら、何も知らない高校生にドンブリ勘定の力学を押し付けることになろう。この問題に関し何度投稿しても、Pseudworkを盾に、高校教科書の仕事は、物体と書かれているが質点に限定した仕事だとか、高校生向けにやさしく書かれているので、正確さを犠牲にしているとか、まともな反論をせずに、Pseudowork!Pseudowork!と、シュプレヒコールを繰り返すだけではこの問題は解決しない。
釈迦に説法かも知れないが、物事を定義するのは他と明確に区別することによって混乱を避けるためである。場当たり的にいかようにも解釈できる定義は、政治や宗教ならともかく、自然科学の世界にはありえない。なぜ、定義するのか、その目的について、編集委員会は既に物理以前の間違いをしている。編集委員会の主張は二重三重に間違えた「屁理屈」としか思えない。
編集委員会は、それでも抗力のする仕事に反対したいなら、これまで何度も指摘してきた図1の問題について、抗力のする仕事を用いない別解を、運動方程式に基づき、具体的に数式を用いて示して頂きたい。教育の名のついた学会なら、出来の悪い学生の答案に✖印を書き込むだけでなく手本となる模範解答を示すべきである。抗力のする仕事は仕事と考えてはならないとか、仕事の定義は教科書ではなく理化学辞典を見よとか、あれは良い、これは駄目だと御託を並べての説教だけで、具体的な解法を示さなければ、反抗期の暇人は益々ひねくれてグレルしかない。
抗力は仕事をするかしないか、これはpseudowork論文以前から議論されてきた仕事のパラドックスだが、Pseudowork論文はそれを解決したことになっていない。抗力は、その作用点が動かないので複合運動にエネルギーを供給することはできないが、一方の運動から他方の運動にエネルギーを移動させるために、抗力は二つの運動に、それぞれ正と負の仕事を同時にしている。これはニュートンの運動法則から導かれる疑いようのない帰結ではないだろうか。
力学現象を数式に頼らずに説明することは物理教育にとって大切なことだが、運動法則から数学的に導かれた結果を無視してはならない。数学が好きでも嫌いでも、直感だけに頼って墓穴を掘らないためには、編集委員会も、図1のような複合問題を、運動方程式から数学を用いて一度は解いてみられることをお勧めしたい。
力学に、なぜ、このような混乱が起き、それがなぜ放置されているのか、それは教養部廃止がその一因になっていないだろうか。高校の力学では、主として単一運動である。大学に入学すると、初等力学を習い、そこで複合運動がでてくる。そのあと、大学では熱力学や解析力学を習う。しかし、教養部廃止後、高校の物理と大学の物理を繋ぐ初等力学を習う機会が少なくなり、仕事Aや仕事A’を習う機会も教える機会もなくなり、仕事Bのみが唯一の仕事との誤解が生まれたのではないだろうか。しかし、それは、図1のような複合運動を運動方程式を作って解いてみればすぐに分かることである。
高校物理の教科書はニュートン力学に基づいて正しく記述されている。もちろんトンデモ本などではない。しかし、物理教育は、40年前に発表された論文の誤りに気付かず、その論文が前提として掲げている誤った命題「抗力は仕事をしない」を何が何でも正当化するために、高校教科書に「トンデモ本」との汚名を着せようとしているのではないだろうか。物理教育は、この問題に関する限り、ニュートン力学を無視した、本末転倒の議論をしていることに気付くべきである。

コメント