運動と仕事とエネルギー
物体が外力を受けながら運動しているとき、物体の並進運動の運動量およびエネルギーは、物体の質量Mと速度vを用いて、それぞれ、MvおよびMv2/2と表されるが、どちらも並進運動の運動方程式から力積および仕事を計算した結果であり、運動方程式なしで、なぜ、そうなるかを説明することは不可能だろう。運動方程式を時間で積分すれば、力の力積として運動量が導かれる。一方、運動方程式に速度を掛けて時間で積分すれば、あるいは同じことだが、運動方程式を物体の重心座標で積分すれば、力のする仕事として並進運動のエネルギーが求められる。同様に物体の回転運動においても、角運動量は、力のモーメントの力積として、また、回転のエネルギーは、力のモーメンとのする仕事として、ともに回転の運動方程式から導かれる。
力積も仕事も、運動方程式が与えられれば、あとは数学的に導かれる概念であるが、仕事の定義については、誤解による混乱が続いているようである。物体の並進運動および回転運動における力学的エネルギーを正しく導くには、仕事は、並進と回転の二つの運動に対して、それぞれ、次のように定義されなければならない。
- 仕事A=力と重心の変位との内積 (1)
- 仕事A’=重心のまわりの力のモーメントと重心のまわりの回転角の内積 (2)
高校物理教科書、広辞苑、ブルタニカ百科事典では、仕事はすべて(1)式で定義されている。(1)式は質点に限定した仕事の定義ではなく、物体一般に対して、力が物体の並進運動にする仕事である。そして(2)は、並進運動に対する仕事の定義(1)を、物体の回転運動に拡張した仕事の定義である。
高校教科書や広辞苑の仕事の定義に対し、理化学辞典では、仕事を、仕事=力と作用点の変位の内積として定義している。これを仕事Bとすると、仕事Aや仕事A’が、それぞれ、並進と回転の運動方程式に則って定義された仕事であるのに対し、仕事Bはエネルギー保存則に則って定義された仕事である。仕事Aは、仕事の対象が質点の場合に限って仕事Bに等しくなるが、一般には両者は異なる仕事である。仕事Aや仕事A’と仕事Bとの顕著な相違点は、抗力でも、仕事Aや仕事A’をすることは可能だが、抗力は作用点が動かないので仕事Bをすることはできない点であろう。仕事Bは力が物体または系にした仕事であり、仕事Bに等しいエネルギーが、外部から物体や系に入り、物体や系全体のエネルギーが増えることを意味している。しかし、仕事Bによって、外部から入ってきたエネルギーが、物体や系内のどのような運動にどう配分されるかは仕事Bだけでは分からない。
斜面を転がる円柱
力学では、仕事Aおよび仕事A’が必要であり、それと仕事Bとの違いを明確にするために、図1のように、質量M、慣性モーメントI、底面の半径rの円柱が、重力と斜面からの抗力Fを受けて転がる場合を考えてみよう。最初静止した状態から斜面方向(x方向)に加速度αで転がり距離Lだけ進んだとき、並進運動の速度vがvLになり、回転の角速度ωがωLなったとしよう。
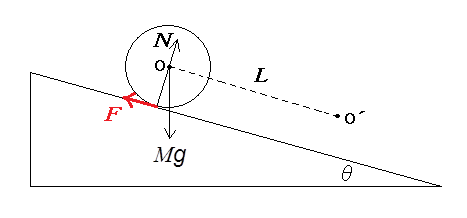
円柱の並進運動および回転運動の方程式は次のように表される。
- 並進運動:Mgcosθ-F=Mα (3)
- 回転運動:Fr=Idω/dt (4)
(3)を重心の座標xで0からLまで積分し、(4)を円柱の回転の角度φで積分すると、rdφ=dx、dφ=ωdtであるから、最初、oに静止していた円柱がo’まで転がると、並進運動および回転運動に対する仕事とエネルギーの式は、それぞれ、
- 並進運動:MgLcosθ-FL=(1/2)MvL2 (5)
- 回転運動:FL= (1/2)IωL2 (6)
となる。(5)式と(6)式は、円柱の並進運動に対し、重力と抗力とが仕事をし、回転運動に対しては抗力のみが仕事をすることを示している。両者を加えると、抗力のした仕事は消え、円柱の全体運動に対する仕事とエネルギーの式は、
- 全体運動:MgLcosθ = (1/2)MvL2 + (1/2)IωL2 (7)
となる。(7)式の右辺は円柱の全力学的エネルギーであり、左辺は重力が円柱の運動にした仕事Bである。左辺は、おもりの位置エネルギーの減少分でもあるので、移項すると円柱の力学的エネルギーの保存則となる。
- エネルギー保存則: (1/2)MvL2 + (1/2)IωL2 ーMgLcosθ = 0 (8)
40年前の一連の論文、例えば、Pseudowork and real work:Am.J.Phys.51(7),July1983 によれば、車の運動に仕事をするのは車のエンジンであり、駆動輪のタイヤが道路から受ける抗力ではないという。エンジンは駆動輪の回転運動に仕事をすることによって車の運動にエネルギーを供給しているが、道路からの抗力がなければ、駆動輪が回転するだけで、車は走れない。抗力が駆動輪の運動に負の仕事して、同時に車の並進運動に正の仕事するから車は走ることができる。しかし、この論文では、真の仕事は仕事Bのみであり、仕事Aは仕事に似て仕事でないPseudowokだという。車に働く水平方向の外力は抗力だけである。その抗力が並進運動や回転運動に仕事をしないで、車はどうやって走れるのだろうか。また、図1の円柱は回転のエネルギーをどのようにして得るのだろうか。(7)式に抗力は現れないが、仕事Aや仕事A’を仕事から排除して、(7)式をどのようにして導くのだろうか。
仕事Bと熱力学
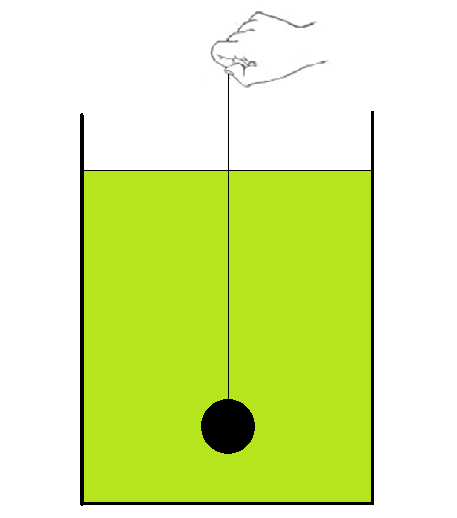
図2のように、液体中のおもりを高さy1からy2まで引き上げるとき、糸の張力の強さをTとすると、張力のした仕事Wは、Tを高さyで積分すればよい。つまり、積分範囲をy1<y<y2として、W=∫Tdyと表される。Wは糸の張力T をその作用点の座標yで積分した値だから仕事Bであり、水とおもりからなる系のエネルギーの変化になる。すなわち、水の運動エネルギー、水の位置エネルギー、おもりの運動エネルギー、おもりの位置エネルギーの、すべての力学的エネルギー和の変化に、さらに発生した熱エネルギーを加えたエネルギーに等しくなる。しかし、糸の張力がした仕事Wが各エネルギーにどのように配分されるかは、Wからだけでは分からず、ゆっくり引き上げるか急激に引き上げるかで異なる。
物理は暗記科目か?
真の仕事は仕事Bだけとし、仕事Aや仕事A’を仕事から除外して、高校生や大学初年次の学生に初等力学をどう教えればよいだろうか。抗力は作用点が動かないという理由で、抗力のする仕事を否定して、物体の並進運動や回転運動のエネルギーをどのようにして導けばよいのだろうか。「エネルギーを運動方程式から導いてはならない。何も考えず、並進運動のエネルギーは(1/2)Mv2、回転運動は(1/2)Iω2と、百篇唱えて暗記せよ」と高校生や学生に教えるべきだろうか。しかし、日本物理学会も日本物理教育学会も、何度投稿しても、抗力のする仕事をタブー視するだけである。仕事Bは熱力学では重要であるが、高校物理で仕事Bが必要なのは、外力がバネに仕事をするときぐらいである。物体の運動を分解して考える力学では、仕事Aや仕事A’が重要な仕事であり、仕事Bはその結果として導かれるので、仕事Bは必ずしも必要ではない。「高校物理教科書は、初心者のために易しく書かれているので、物体にする仕事と書かれているが、本当は質点に対する仕事の定義だ」とか、「高校物理の仕事を物体一般に適用するとPseudoworkになる」とか、日本物理学会も日本物理教育学会も、この問題に関する限り、常軌を逸した支離滅裂な回答しか返してこない。40年前のPseudowork論文に集団洗脳され、思考停止に陥っている両学会が正常な判断力を取り戻してPseudoworkと決別し、力学教育がニュートンの運動法則に基づいた本来の姿に立ち戻ることを期待したい。

コメント