1. はじめに
これは、「深く考えてはいけない問題?」の補足のつもりだが、どちらを先に読んでいただいても構わない。水槽中に糸で吊るされたおもりを引き上げるときの糸の張力、液体からおもりに働く浮力、同じく重りに働く粘性抵抗はどのような役割をしているだろうか。糸を引き上げるためにした仕事は、外部から、おもりと液体からなる系に、その仕事に相当する力学的エネルギーが入ってきたことを意味し、系の全エネルギーがその分だけ増す。つまり、糸の張力は、系に仕事をする。それに対し、浮力も粘性抵抗も、おもりと液体との間に働く内力であり、その仕事は系の全エネルギーには寄与しないが、おもりと液体の間でのエネルギーのやり取りに寄与する。
2. 準静的に引き上げる場合
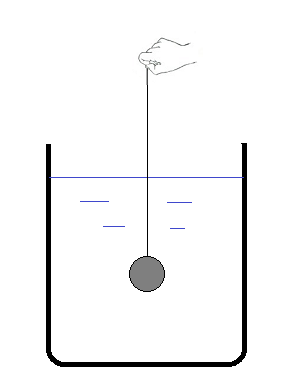
密度ρの液体中に質量M、体積Vのおもりが糸で吊り下げられて静止しているとする。重りに働いている力は、重力Mg、浮力ρVg、それに糸の張力Tである。つり合いの式から、次のようにT を求めることができる。
T=Mg‐ρVg ①
張力Tは一定だから、釣り合いの状態①を保ちながら、ゆっくり、つまり、準静的に高さhだけ引き上げると、そのとき糸の張力がする仕事Wは、Tとhの内積であるから、
W=Mgh ₋ ρVgh ②
となる。②は張力Tがした仕事の分だけ、おもりと液体からなる系のエネルギーが増すことを示し、右辺第1項はおもりの位置エネルギーの増加分であり、第2項は液体の位置エネルギーの減少分である。つまり、右辺全体は、系の位置エネルギーの増加分である。②の右辺第2項を移行して、
W+ρgh=Mgh ③
と書き換えると、張力Tがした仕事Wと、浮力ρVgがした仕事ρVghとの和が重りの位置エネルギーの和になることをしめしている。系を重りと液体に分けて考えると、液体が、浮力ρVgによっておもりに仕事 ρVghをしたために、液体はその分だけ位置エネルギーを失っている。この場合、準静的運動であるから、おもりの運動エネルギーは存在せず、おもりに粘性抵抗は働かず、液体に運動エネルギーも生じない。
3. 一定の速さで引き揚げる場合
次におもりを一定の速さvで引き上げよう。高さhを引き上げるのに要した時間をtとすると、h=vtである。おもりに働く力は、張力T 、重力Mg、浮力ρVg、それに粘性抵抗である。粘性抵抗が、速さvに比例するとして、その比例係数をkとすれば、粘性抵抗はkvと表される。おもりの速さは一定であるから加速度は0である。おもりの運動方程式より、Tが求められ、
T=Mg–ρVg+kv ④
となる。この場合も張力は一定となるが、準静的に引き上げた場合より粘性抵抗の分だけ大きくなる。重りが高さhだけ増したとき、張力のした仕事Wは、④より
W=Mgh ₋ ρVgh +kvh ⑤
となる。右辺第1項はおもりの位置エネルギーの増加分、第2項は液体の位置エネルギーの減少分、第3項は、高さhだけ引き上げられる間に粘性抵抗によってなされた仕事であり、h=vtから、kv2tとなる。単位時間当たりに粘性がした仕事は、速さの2乗に比例するが、この場合、速さvは一定であるので単位時間当たりの粘性の仕事は一定である。おもりは一定の速さで運動するのでおもりの運動エネルギーの変化はない。また液体にも流れが生じるが、定常流だから、液体の運動エネルギーの変化もない。おもりの運動は、粘性抵抗によって、エネルギーを失うが、その分、熱となる。②とくらべれば、⑤では、粘性抵抗による発熱量の分だけ張力は多くの仕事をしなければならない。
4. 一定の加速度で引き上げる場合
おもりを液体中に静止した状態から一定の加速度αで引き上げる場合、おもりを引き上げ始めて、時間tが経過したときのおもりの速さvは、v=αtであり、微小時間dtの間に、おもりが引き上げられた高さdhは、dh=vdt=αtdtとなる。この場合、おもりの速さが変化するので、糸の張力Tは一定でなく、
T=Mα+Mg–ρVg+kv ⑥
となる。⑥の両辺にdh=vdtを掛けると、dt時間に張力が系にした仕事dWが求まる。つまり、
dW=Mαdh+Mgdh–ρVgdh+kv2dt ⑦
ここで、右辺第1項は、
Mαdh=Mα2tdt=d[(M/2)α2t2]=d[(M/2)v2]
となるので、⑦は
dW= d[(M/2)v2 +Mgh]-ρVgdh+kv2dt ⑧
となる。⑧の右辺第1項はおもりの力学的エネルギーの増分である。第2項は液体の位置エネルギーの減少分、第3項は粘性抵抗による仕事であり、それは液体の運動エネルギーと熱になる。今度の場合は速さvが時間に比例して大きくなるので単位時間当たりの粘性抵抗による仕事は時間の2乗に比例して増加し、それは液体の運動エネルギーを通して最終的には熱となる。
5. おわりに
上記三つの例のいずれの場合も張力は、おもりと液体からなる系に仕事をして、その分、系全体のエネルギーを増加させ、浮力と粘性は、おもりと液体のあいだでのエネルギーのやり取りに寄与している。液体はおもりに浮力を及ぼし仕事をすることによって、おもりの力学的エネルギーを増すかわりに、液体はその分、自身の位置エネルギーを失っている。また、液体は、おもりに粘性抵抗を及ぼし、おもりに負の仕事をするかわりに、液体自身に運動エネルギーと熱を発生させている。通常の液体であれば、浮力が存在すれば粘性も存在する。しかし、「深く考えてはいけない問題?」 におけるおもりAの運動では浮力は存在するが、粘性は無視できるとしている。その仮定が成り立つのは2~4のうち、おもりが準静的に液体中を動く、2の場合だけである。おもりが有限な速さで動けば、液体の運動を無視することはできない。3と4の場合、粘性が無視できるのは、液体の密度が無限小の場合であり、そのときは、当然、浮力の大きさも無限小でなければならない。

コメント