高校の教科書には、仕事は、物体に働いた力と物体の変位の積として定義され、一方、岩波書店の理化学辞典には、仕事は、力学系に力が働いたとき、力とその力の作用点の変位との積とされている。前者の仕事を仕事A、後者を仕事Bとし、ベクトルの内積を表す記号・を用いると、仕事A,Bは、それぞれ、[仕事A=力・重心の変位]、および[仕事B=力・力の作用点の変位]と表され、両者の違いは、力との内積の相手が、物体の重心の変位か、力の作用点の変位かの違いである。
仕事の対象が質点の場合、重心と力の作用点は同じだから、仕事Aと仕事Bとは同じになるが、物体一般に対しては、仕事Aは、外力が物体の並進運動に対してした仕事であり、つまり、外力が仕事Aをした分だけ、物体の並進運動の力学的エネルギーが増す。それに対し、仕事Bは、外部の動力源から系や物体に入ってきたエネルギーに等しくなり、一般には、そのエネルギーは系内で力学的エネルギーと熱エネルギーになるが、熱の発生がない純粋に力学的な系、例えば、円柱が外力を受けころがり運動をする場合にも、仕事Bによる力学的エネルギーが、並進運動と回転運動にどのように配分されるかは仕事Bだけからは分からない。つまり、仕事Bによるエネルギーがどのように使われるか、その内訳を知るには系の運動の詳細に立ち入らなければならないが、そのとき、仕事Aが必要になる。
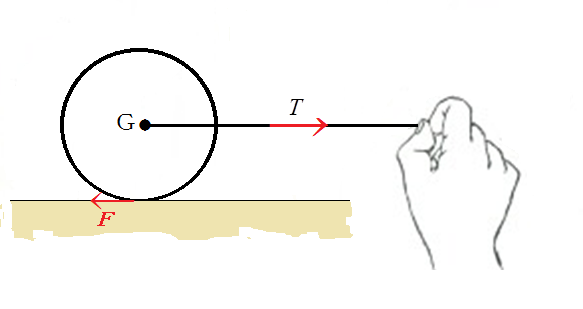
図1のように、台上に静止している円柱に力Tを加えてdxだけ引っ張ると、仕事BはTdxとなる。円柱が台から受ける水平抗力Fは静止摩擦力であり、その作用点は動かないので、仕事Bには寄与しない。Tが円柱に仕事Bをした結果、円柱の力学的エネルギーはTdx だけ増すことになるが、その力学的エネルギーが、円柱の二つの運動、つまり並進運動と回転運動とに、それぞれどのように配分されるだろうか。
エネルギーの内訳を知るにはそれぞれの運動に対する仕事を考えなければならないが、その仕事はそれぞれの運動方程式から数学的に導かれる。並進運動および回転運動の運動方程式は、それぞれ、
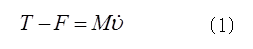

であるから、(1)の両辺に重心の変位dxをかけ、(2)の両辺に円柱の回転角の変位dθをかけると、(1)の右辺は並進運動のエネルギーの増し分、(2)の右辺は回転運動のエネルギー増し分になるから、(1)の左辺(T-F)dxは並進運動に対する仕事であり、これは仕事Aであるから、dxは作用点の変位でなく、重心の変位と考えるべきである。また、(2)の左辺は回転運動に対する仕事であり、力のモーメントFaと円柱が回転した角度dθの積、つまり、一般化力と一般化座標の変位の積であるから、一般化された仕事Aであり、結果はFdxに等しくなる。(1)と(2)から、二つの運動になされた仕事が分かったので両者を加え合わせると、全体の仕事はTdxになり、これはTがした仕事Bになる。回転軸などに摩擦熱が発生する場合には、二つの運動の力学的エネルギーの和に内部で発生する熱エネルギーまで加えた値がTdxに等しくなる。
仕事Bは外部の動力源から系に入ってくるエネルギーであるから熱力学にとって重要な仕事であるが、運動を分解して考える力学では、運動方程式から個々の運動に対する仕事が分かり、その合計から仕事Bが分かるので、熱の発生を考える必要のない純粋に力学的な系では仕事Bは重要ではない。しかし、逆に仕事Bだけが分かり、その内訳を示す並進運動や回転運動に対する仕事が分からなければ、全収入と全支出だけを記載し支出の内訳が記載されていない会計報告書のようなものである。高校教科書に、仕事Bでなく仕事Aが記載されているのは、力学にとって仕事Aのほうが重要だからである。
図1では円柱の運動に力学的エネルギーを供給する動力源は外部に存在しているが、次の図2の場合には、人と自転車を一つの系と考えると、動力源は系の内部に存在する。
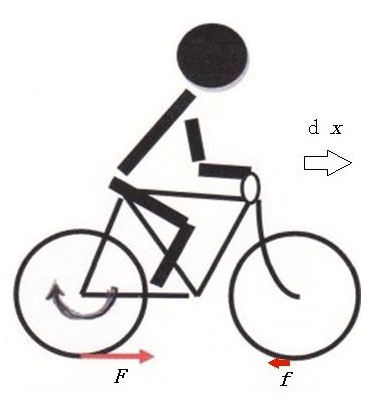
自転車が加速するときの動力源は筋力であるが、内部の動力源がする仕事は、仕事Aでも仕事Bでもなく、力学の範疇ではない。それでも、筋力で作り出された力学的エネルギーが、結果的に系全体のエネルギーになるので、筋力が仕事をして、そのエネルギーで自転車が加速するのは間違いないが、それだけでは、そのエネルギーがどのようにして系の細部に伝わるかが分からず、ドンブリ勘定の域をでない。この場合も仕事Aを用いて説明すれば、エネルギーの伝達が明快になる。
筋力の仕事によって人体に変形運動が生じ、その変形運動によって人はペダルを踏み、チェーンを通して後輪が回転するが、後輪の回転のエネルギーが、そのあと、どのようにして、系の並進運動や前輪の回転運動になるかを説明する必要がある。道路から受ける水平抗力Fが存在しなければ、いくらペダルを踏んでも後輪が回転するだけだが、Fが存在すれば、Fは後輪の回転運動に負の仕事をするとともに、系の並進運動に正の仕事をする。自転車の道路から受ける抗力が仕事をしても、そのエネルギーを道路が供給しているのではない。並進運動が加速されると、さらに前輪に水平抗力fが後ろ向きに働き、fは並進運動に負の仕事をし、前輪の回転運動に正の仕事をする。エネルギーの伝搬を説明するには、図2の場合も図1の場合と同じく仕事Aが必要になる。
宇宙ステーションのなかで、他と触れ合うことなく静止している宇宙飛行士がいくら手足を動かしても、また体をねじっても折り曲げても飛行士に並進運動は生じない。しかし、飛行士が宇宙ステーションの壁を押すと、飛行士は壁から反作用力を受け並進運動が生じる。この場合も、壁からの反作用力はその作用点は動かないが、飛行士の変形運動に負の仕事をして飛行士の並進運動に正の仕事をする。
アメリカで40年ほど前に発表された一連の論文では、仕事Bが唯一、真の仕事であり、外力と重心の変位との内積、つまり、抗力のする仕事を含む仕事Aはエネルギー保存則に反する仕事として、真の仕事でなく、Pseudoworkとされた(Am.J.Phys.51(7),July(1983)p.597)。しかし、抗力が仕事をしてもエネルギー保存則に反することはない。いかなる場合も抗力は仕事をしないという間違った先入観に囚われ行き詰っているところに、救世主のように現れたPseudoworkの考えに幻惑され、昔も今も物理教科書や辞典類に明記されているうえに、運動方程式から自然に導かれる仕事Aをpseudoworkとして力学から排除し、仕事Bのみを真の仕事としたのでは、収入だけは分かっているが、使途不明のまま収支が一致し、繰越すことなく、きれいさっぱり、なくなる我が家の家計と同じになる。
科学に試行錯誤は避けられないが、仕事Aを否定したのでは、高校物理が混乱するだけでなく、人類の至宝であるニュートン力学はドンブリ勘定の力学になろう。簡潔で美しいニュートン力学の理論体系を損なうことなく、仕事に関する40年来の問題を解決するには、仕事Aを真の仕事として復活させ、動力学において抗力は正と負の仕事を同時にしていると考えるべきである。抗力のする仕事は偏屈老人の妄想の産物ではない。すでにニュートンが、その遺産である運動の基本法則のなかで、我々に懇切丁寧に説き教えていることの一つであろう。それでもなお40年前の論文を盾に、抗力はあくまでも仕事をしないとして、仕事Aを否定し、仕事Bだけで力学を説明しようとする挑戦的なラ・マンチャの精神は称賛したいが、その無謀な試みに勝算はなかろう。
運動法則から数学的に自然に導かれる仕事Aを否定することは、運動法則そのものを否定する暴挙であろう。Pseudoworkの考えは、完成したニュートン力学に無理に余計な手を加えようとして足が出た「勇み足」だったのではないだろうか。

コメント