動かない道路や壁から受ける力、つまり、作用点の動かない抗力が仕事をすると言えば、初等力学も理解できずに、定年退職までどんな物理を学生に教えてきたのだ、そんな非難があるのも当然であろう。それでも敢えて、抗力のする仕事の必要性とその利点を、ネット上の我が墓石に刻み、広く世に伝えたい。いかなる場合も抗力は仕事をしないとする、日米共通の常識?を覆すことができるか、それとも力学的には何の根拠もない、間違った岩盤規制によつて跳ね返されるのか、抗力の仕事の是非を巡る「仁義なき戦い」も、いよいよ最終章。コロナ自粛のなかで迎える年末年始にオンラインでお楽しみを!
1. はじめに
リンゴが落ちるのは、リンゴに重力が働くからである。それなら、地面に落ちた後も、リンゴには重力が働いているのに、リンゴはなぜ地面の上に静止しているのか。それはリンゴに地面から上向きの力、抗力が働き、それが重力とつりあっているからである。しかし、重力および地面からの抗力は我々人間にも働き、人が動けば、人に働く重力と抗力は、必ずしもつり合わない。抗力は静力学でのつり合いを説明するだけでなく、動力学の運動方程式にも現れる。それでも抗力は仕事をしないだろうか。
動力学においても、抗力は、その作用点が動かないので、一切、仕事をすることはないとする、日本物理学会および日本物理教育学会の見解に対して、正味の仕事をすることはできない抗力も、運動を並進運動とそれ以外の運動に分解すれば、分解された二つの運動に、それぞれ、正と負の仕事をしていることを主張したい。
2.運動の分解と合成
力学では、一般に、物体の運動を並進運動と重心に相対的な運動とに分解して考えることができる。とくに、物体が剛体の場合には、並進運動と重心のまわりの回転運動とに分解できる。
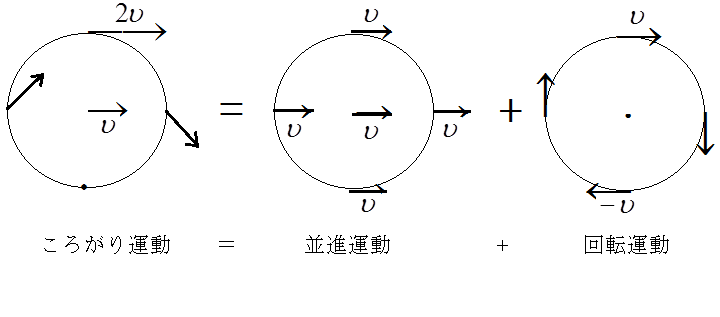
図1のように、円板や円柱が水平な台上を滑ることなくころがる運動を分解すると、並進運動では、すべての点が同じ方向に同じ速さで動き、回転運動では、重心は静止し、円周上の点が接線方向時計まわりに速さ
で動く。逆に、並進運動と回転運動とを合成すると、ころがり運動となり、円周の一点が、台と接触した瞬間、並進運動における速度と回転運動における速度とが打ち消し合い、その速度は0となる。その後、円周上を半周し、最高点に達したとき、並進運動と回転運動の速度が同じになるから、最高点での速度は、2
となる。図1のように、円柱が右方向に転がるとき、円柱の床との接点は、ころがり運動に対しては動かないが、運動を分解すると、並進運動に対しては右方向に動き、回転運動に対しては左方向に動くと考えなければならない。そうでなければ運動を分解することはできない。
3. 円柱の運動と仕事
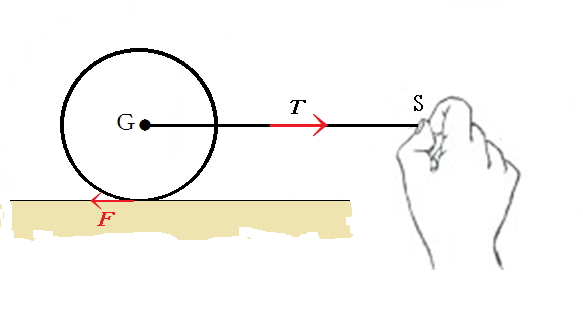
次に、円柱に外力を加えて円柱をころがす場合を考えてみよう。図2のように質量、慣性モーメント
、半径
の円柱の重心に、外部の動力源が力
を加えて引っ張り、円柱が水平な台上を滑ることなく転がるとき、円柱は台から左向きに水平抗力
を受ける。円柱が転がって進む速さを
、回転の角速度を
とすると、滑らないという条件から、
が成り立つ。円柱のころがり運動を、並進運動と回転運動とに分解したとき、それぞれの運動方程式は、
並進運動: (1)
回転運動: (2)
となる。微小時間間隔をとして、(1)式の両辺に並進運動の微小変位
をかけ、(2)式の両辺に回転運動の微小回転角
をかけると、
(3)
(4)
となる。(3)と(4)式は、力が並進運動に対し仕事をし、一方、水平抗力
は並進運動に負の仕事をし、同時に回転運動に正の仕事をする。水平抗力が負と正の仕事を同時にすることによって、並進運動から回転運動にエネルギーが移動する。(3)式と(4)式を加えると、
(5)
となる。(1)式と(2)式から、(3)と(4)式を経由して、(5)式を導いたが、そのどこかに不都合な点があるだろうか。
先に(1)と(2)式から、水平抗力を消去したあと、仕事の式を求めても、同じように(5)式を導くことができる。どちらの方法も正しいが、両者とも、(1)式と(2)式で示されるように、ころがり運動が二つの運動に分解できることを前提にしている。運動を分解する前のもとの運動に対して抗力の作用点は動かないが、分解された二つの運動に対しては、すでに図1に示したように、抗力の作用点は互いに逆向きに動いている。
4. 自転車
円柱の運動では、動力源は系外に存在していたが、図3のように、人が自転車に乗って走るとき、人と自転車を一つの系と考えると、動力源は系内に存在する。この場合も系の運動を系の並進運動と系の重心に相対的な運動の和に分解することができる。
系の並進運動では、人を含めた系の全ての点が、重心と同じ速度で平行運動をし、人は変形運動をすることはできない。変形運動ができなければ、当然、人の筋力は系の並進運動に仕事をすることはできない。系の並進運動に仕事をすることができるのは、自転車のタイヤが道路から受ける水平抗力だけである。しかし、重心に相対的な系の運動に対しては、人自身も変形運動をすることができるから、筋力は系の変形運動に仕事をすることができる。
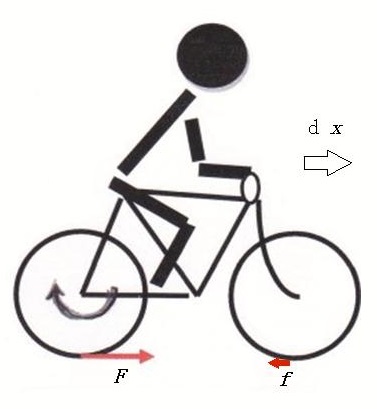
人は自らを変形させることによって、ペダルを踏み、チェーンの運動を通して、後輪の回転運動に仕事をする。後輪の回転速度が増せば、後輪のタイヤには、道路から進行方向に水平抗力が働く。水平抗力
は後輪の回転運動に負の仕事をすると同時に系の並進運動に正の仕事をする。その結果、並進運動の速度が増せば、前輪のタイヤに、水平抗力
が後ろ向きに働き、並進運動に負の仕事をするとともに、前輪の回転運動に正の仕事をする。系に力学的エネルギーを供給したのは当然系内の動力源である人の筋力である。
人は飯を喰らい糞して走る。車は燃料を使い排気ガスや廃熱を放出して走る。熱力学的には正しいが、道路を走れる理由の力学的な説明としては、それだけでは不十分ではないだろうか。
5. 垂直抗力
図4のように、水平な床の上で質量の人が立ち上がるとき、人の重心Gに重力
が働き、床から上向きの抗力
を受ける。重心の高さを
、立ち上がるときの重心の上向きの速さを
とする。
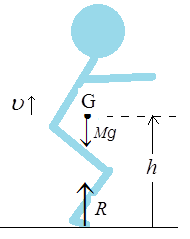
この場合も立ち上がり運動を並進運動と変形運動に分解して考えることができる。微少時間における重心の微少変位は
であるから、並進運動では、重心のみならず床から抗力を受ける足の裏も、上向きに
だけ変位することになる。並進運動についての仕事とエネルギーの式は、
(6)
となる。
次に、重心に相対的な運動、この場合は人の変形運動だが、それについて考えよう。変形運動に対して人の重心は動かず、足の床との接点が下向きに変位する。変形運動のエネルギーをとすると、微小時間
におけるその変化量
は次の式で表される。
(7)
ここで、右辺第1項は筋力が人の変形運動にした仕事であり、第二項、
は抗力が変形運動にした負の仕事である。(6)と(7)式から
を消去し、
=
と置きかえると、
(8)
となる。自転車と同じく、この場合も内部の動力源である筋力が仕事をして変形運動が生じると、抗力は、(7)式のように、変形運動に負の仕事をすると同時に、(6)式のように、重力場のなかでの並進運動に正の仕事をして、(8)式が成り立ち、人は自らの筋力から力学的エネルギーを得て立ち上がることができる。
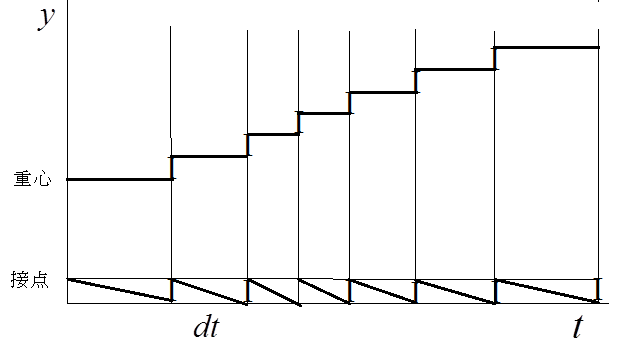
そのときの、重心の運動と、床との接点の運動を図示すると、図5のように、床と足の接点はのこぎり刃状の変化をし、重心は、段差がの階段状の変化をすることになる。しかし、
→0の極限では、接点は動かず静止し、重心の高さを表すグラフは変化率が
の滑らかな曲線に収束する。
無重力空間で宇宙飛行士が、いくら手足を動かしても、外部から抗力を受けなければ並進運動が生じることはない。内力は、変形運動に対して仕事をすることはできても、並進運動に直接仕事をすることはできない。抗力がなければ、筋力がした仕事によって生じた手足の変形運動は熱に変化するだけで、並進運動は生じない。しかし、飛行士が宇宙船の壁に触れ、飛行士に抗力が働けば、抗力が飛行士の変形運動に負の仕事をし、同時に並進運動に正の仕事をすることによって、変形運動が得たエネルギーの一部を並進運動のエネルギーに変えることができる。
6. 仕事の定義
ここで仕事の定義について考えてみよう。高校生が初めて動力学を学ぶ高校の物理教科書には、仕事を次のように定義している。
「物理では、物体に力を加えて、力の向きに物体を移動させたとき、力が仕事をしたという。物体に一定の大きさF[N]の力を加え、力の向きに距離s[m]移動させたとき、力が物体にした仕事Wは次のように定められる。W=Fs (仕事[J]=力の大きさ[N]×移動距離[m])」 :第一学習社「基礎物理」より。
他の出版社の高校の物理教科書、大学初年次の物理教科書、広辞苑の定義も、さらにブルタニカ百科事典でも同様な定義である。
一方、岩波書店の理化学辞典(第3版)では、仕事を次のように定義している。
「力学系に力が作用し作用点がdsだけ変位するとき、スカラー積(F,ds)を、その力が力学系になした仕事という。」
便宜上、教科書や広辞苑などによる仕事の定義を定義A、理化学辞典による仕事の定義を定義Bと呼ぶことにすると、仕事の対象が質点の場合には、二つの定義は一致する。しかし、定義Aが、物体を質点の場合に限定した仕事の定義であるなら、定義Aの記述のなかの物体は質点と書くべきである。また、定義Bが物体一般に対する唯一の仕事の定義だとするなら、高校の物理教科書にも、定義Aでなく、定義Bを掲載するべきである。質点という用語も、力の作用点という用語も高校物理ではすでに使用されている用語である。
概念を明確に区別するための定義に、物体と質点とが混同されていては定義する意味はない。それは力学以前の問題であろう。定義Aも定義Bも質点を含めた物体一般に対して外力がする仕事の定義であるが、前者は物体の並進運動に対する仕事の定義であり、後者は物体の全ての運動に対しての仕事の定義である。
円柱のころがり運動の例では(3)式が仕事Aであり、(5)式が仕事Bである。仕事Aも仕事Bも外力のする仕事であるので、立ち上がり運動に対する(8)式は、内力のする仕事だから仕事Aでも仕事Bでもない。
しかし、pseudoworkは、その後に発行された辞書の仕事の記述に混乱をもたらしているようである。2005年に発行された培風館の物理学辞典は定義Aと定義Bとを混同し、仕事を次のように定義している。
「物体に力を加えて、物体が力の向きに移動したとき、力は物体に仕事をしたと言い仕事の量は力と移動距離の積で与えられる。一般には、力の向きと物体の移動の方向は必ずしも一致しないので、物体または力学系に外力Fが作用し、作用点がdsだけ変位したとき、仕事は両者のスカラー積、F・ds=Fdscosθである。」
物理学辞典での仕事の定義の前半は物体の並進運動に対する仕事の定義であり、「一般には」以降の後半は物体の全体運動に対する仕事の定義である。定義Aと定義Bとを切り貼りしてつないだために、意味不明の木に竹を接いだような記述になっている。
7. おわりに
木だけを見れば抗力が仕事をしているように見え、森だけ見れば抗力は隠れて見えない。しかし、木を見て森を見て再び木を見れば、抗力のする仕事が必要である。
抗力は作用点が動かないので、一切、仕事をしないという固定観念が、40数年前に、力学教育にpseudoworkという、仕事のようで仕事でない、いわば仕事の幽霊を生み出したようだが、教科書などに定義されている仕事Aはそれ以前から存在している仕事の定義である。しかし、それをpseudoworkとして仕事から排除したのでは、運動を分解して、仕事とエネルギーを考えることができなくなり、力学の発展の歴史に逆行することになろう。ニュートンのプリンキピアから300年以上が経過し、古典力学は既に完成した学問であり、今日の力学に、pseudoworkのような得体の知れない仕事が入り込む余地はない。
追記. 愚者の提言
「天は人の上に人を造らず、人の下に人を造らず」とは全ての人を指すのではないのか、「法の下での平等」とは生まれながらに、誰それの区別なく、全ての人に与えられているのではないのか、仕事の定義の「物体」とは物体一般を意味するのではないのか、それを「質点」にすり替えてもよいなら、定義する意味はない。しかし、愚者の度重なる投稿に、日本物理学会および日本物理教育学会は、まるで国会答弁のように、繰り返し次のように宣まう。
- 抗力は、その作用点が動かないので仕事をすることはできない。
- 抗力が一見仕事をしているように見えるが、それは真の仕事ではなくpseudoeorkである。
- 高校物理教科書での仕事の定義に記述されている物体とは、物体一般を指しているのではなく、質点に限定していると考えられる。
我が耳目を疑いたくなるような回答だが、これでは、ニュートンだけでなく「学問のすすめ」の福沢諭吉先生も草葉の陰で呆れ果てていよう。聖書の記述に反するとして、進化論やビッグバン理論を否定する創造論者のように、日本の両学会は、アメリカの物理学会に忖度しているのか、今では物理教育関係者にもほとんど知られていないアメリカ発の怪しげな学説を盾にして、抗力のする仕事に頑迷に反対する。それなら運動を分解することも罷りならぬと宣まうのだろうか。森を見るのに、そのなかの木々の動きを見てはならぬのだろうか。
抗力が仕事をすると考えても力学的に不合理なことは何も生じない。仕事Aも仕事Bも、その定義を変更する必要はない。教科書に定義されている仕事Aは、エネルギーを伝えるために必要な仕事である。仕事Bだけではドンブリ勘定になり、エネルギーの流れの仕組みがわからない。
日本の物理教育に君臨する学会が、誤った学説に集団洗脳され、理の追求を放棄して、森を見て木を見ず、安易に仕事Bのみを真の仕事だとし、仕事Aを仕事の範疇から排除するために、高校の力学を質点のみの力学に限定するという場当たり的選択をするなら、人や車が走るという日常のありふれた運動さえも説明できず、高校の力学は受験以外にはほとんど無用な学問となろう。
まだナビが普及していない頃、知らない所を車で走ると、運転手が道を間違え行き止まりになることが度々あった。長崎は坂が多く途中で道が途切れ、その先は石段か、細い山道のどちらかである。道を間違えることは誰にもあることだが、その間違いは無駄ではない。行き止まりに気づけば、もとの大通りまで引き返して別の道を探すことができるからである。ニュートンの運動法則というカーナビがあるのに、それを無視し、既に行き詰った学説に固執して間違えた道を突き進むのは、石段の道を車でくだり降りるような愚行であろう。今一度、力学の原点に立ち戻り、仕事と抗力について虚心坦懐に考えるときではないだろうか。これまで多くを間違えてきた愚者からの提言である。

コメント
すでにメールで私の意見を送った中山正敏です。この問題は根深いと思います。抗力とは何か、静力学、動力学ではどうか、仕事は何か、エネルギー源とは何かなどなど。従来の力学、特に大学基礎教育レベルでは、質点の力学から始めてきれいに体系付けをしています。しかし、それが過度になったために、あなたが体験されるような理不尽な目に合われるわけです。これに対しては、より「自然な」体系化を考えるべきだと思います。そうして「自然の」問題を考える。例えば、質点はまことに不自然な概念です。特に「点」というのが数学的に大きさが「ない」とされてりるために。「ない」のではなくて、大きさを持つ効果を「無視する」とうのが正しい。あなたが言われるように、並進運動のみを考える近似概念です。そういうものから数学的に体系を組み立てようとするから、不自然なものとなり、なまじ考える学生生徒や教師が混乱するのです。ニュートンはもっと自然に考えていました。
1936年生まれの私ですが、あなたと同じぐらいは元気です。それで、提案ですが、「自然な」力学体系づくりを一緒にしませんか?まずは、あなたが考えられたこと、またブログなどで訊いた意見などを整理しませんか?
コメント有難うございます。強力な味方が現れ心強い限りです。抗力の仕事に、なぜこだわるのか、それに関して以下に述べておきます。天井から重りを吊るして振り子を作ると、吊るしただけでは、糸の張力は重力と釣り合っているだけで、当然、仕事をしません。重りを振らしても、やはり張力は仕事をしません。しかし、その理由は、張力の作用点が動かないからでなく、張力と重りの運動方向とが垂直だからです。次に公園のブランコを思い浮かべて下さい。幼い子がブランコに乗り、母親がこどもを押して揺らしています。その場合も、ブランコの鎖の張力は、振り子の糸の張力と同じく仕事をしません。仕事をしているのは、母親が、こどもを押している力です。ところが隣のブランコでは、少し大きなこどもが一人でブランコを振らしています。今度はそのこどもに働く鎖の張力と重心の移動方向とは必ずしも垂直ではありません。その場合は、鎖の張力はこどもの重心運動に仕事をすることができます。しかし、こどもと鎖とを一つの系と考えると、重力場の中の系に働いている外力は鎖を支えている支点から受ける力だけです。振り子を支えている天井が動かないように、ブランコの支点も動かないので、系全体には仕事をしません。それなら、子どもの重心運動の力学的エネルギーはどこから来たのか、それはこどもの変形運動からきているはずです。鎖の張力はこどもの変形運動を妨げています。つまり、鎖の張力は変形運動に負の仕事をすることによって、重心運動に正の仕事をしていると考えるのが一番自然ではないでしようか。もちろん変形運動に仕事をしてエネルギーを供給しているのは人の筋力であることには変わりありません。ブランコについては、「ブランコとボタフメイロ」を参照して下さい。
質点と見なせるかどうかは対象とする系の大小によるのではなく、原子核でも質点と見なせない場合もあれば、惑星でも質点と見なせる場合もありますが、抗力も、作用点が動かないという理由だけで、押し並べて、一切仕事をしないというのでは、力学から物語は消え、ドンブリ勘定の力学になってしまいます。賛否に関わらず、多くの方にご意見を寄せて頂くことを期待しています。