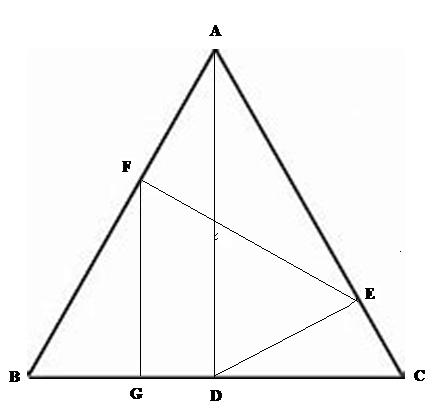
一辺の長さが1の正三角形ABCの頂点Aから、辺BCへの垂線ADを引いたときBDの長さを とする。次に、Dから辺CAに下した垂線をDEとし、CEの長さを
、Eから辺ABに下した垂線をEFとし、AFの長さを
というように、同様の手続きを繰り返すとき、極限値
を求めよ。(T大学大学院入試過去問)
解説 AF=AE/2=(AC-CE)/2 より、 =(1-
)/2、一般に、
=(1-
)/2 となることが分かる。さらに、
-c=k(
-c ) とすると、c=1/3、k=-1/2、よって数列
-c は、公比が-1/2の等比数列だから、n→∞で0に収束する。よつて数列
は1/3に収束する。
大学入試レベル!T大学大学院入試恐れるに足りず

コメント