氷上のチェスと呼ばれるカーリングを一定の角速度で回転するアイスリンクの上で行ったらストーンの運動はどうなるだろうか。リンクとストーンの間に摩擦がなければ、ストーンは慣性系のなかを等速直線運動をするが、回転リンクの上から見れば、ストーンの軌跡は曲線となる。
回転系から見たストーンの軌跡を実験的に求めるには、一般に、電動回転円盤、ストロボ装置、カメラなどの装置が必要となるが、そのような高価な装置を用いないで、それと同じものを、作図によって簡単に求める方法を考えてみよう。
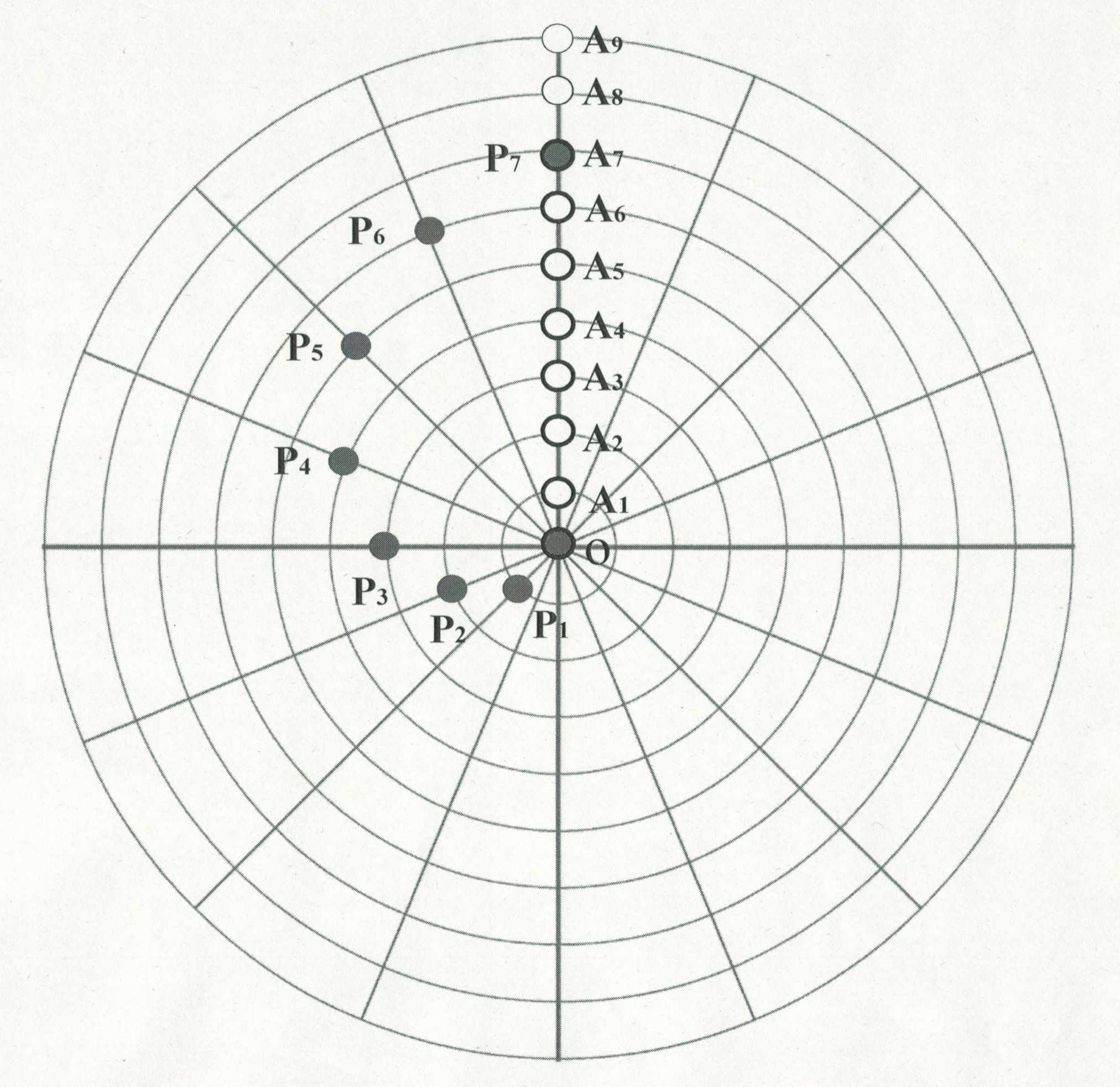 まず、極座標グラフ用紙と、それを、OHP用紙などの、透明な用紙にコピーした極座標グラフを準備する。透明のほうの極座標グラフ用紙を慣性系として用い、直線状の等間隔に並んだ穴を開けておく。もう一枚の極座標グラフ用紙を回転座標系として用い、その上に、穴を開けた透明な慣性系の原点を一致させて重ねる。
まず、極座標グラフ用紙と、それを、OHP用紙などの、透明な用紙にコピーした極座標グラフを準備する。透明のほうの極座標グラフ用紙を慣性系として用い、直線状の等間隔に並んだ穴を開けておく。もう一枚の極座標グラフ用紙を回転座標系として用い、その上に、穴を開けた透明な慣性系の原点を一致させて重ねる。
ストーンが慣性系グラフの穴を一つずつ進むごとに下に敷いた回転系グラフを一定の角度ずつ左回転させながら、穴を通して、ストーンの位置を下の回転座標系にプロットすると、そこに回転座標系から見たストーンの軌跡が点列として記録される。
例えば、質点が原点から等速直線運動を開始したとすると、慣性系では、一定の時間間隔ごとの質点の位置は、図のように、O→A1→A2→A3→…と穴を進んでいく。このとき、回転座標系には、O→P1→P2→P3→・・・と記されていくことがわかる。上から見て、反時計回りに回転する座標系では、進行方向に対して右に曲がりながら進み、さらに質点が原点から遠ざかるにつれ、質点の速さが速くなる。このことから回転座標系では、コリオリの力と遠心力が働いていることが分かる。
次にリンク上の氷に、中心から外に向かって直線状の溝を掘り、その氷の溝の中をストーンを滑らせるという思考実験を試みてみよう。但し、その場合は、リンクは動力なしで、慣性だけで、反時計まわりに回転しているとする。そのとき、リンクの回転はどのように変化するかを考えてみよう。
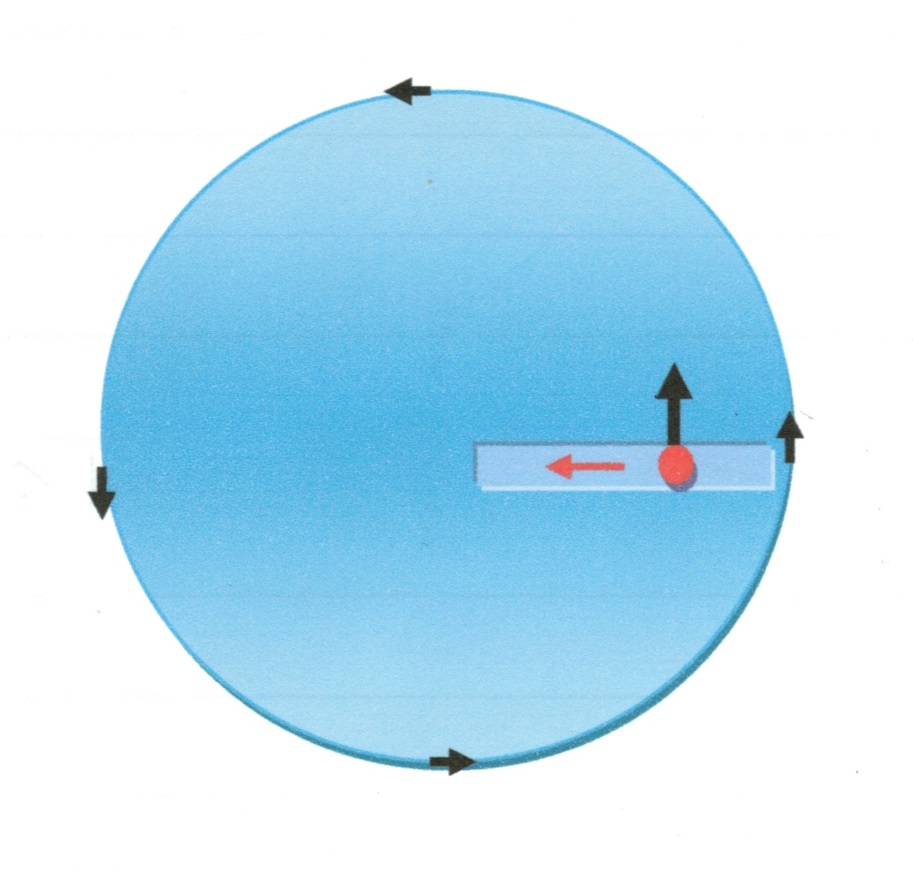 左図のように、ストーンが溝のなかを、中心に向かって滑れば、ストーンはコリオリの力のため、右に曲がろうとして溝の壁を回転と同じ向きに押すので、リンクの回転は速くなると考えられよう。また、逆に、中心から遠ざかるように滑らせると、ストーンは溝の壁を、リンクの回転と逆向きに押すので、リンクの回転は遅くなるだろう。つまり、ストーンが中心に近づけば、リンクの回転は速く、遠ざかれば遅くなる。これは角運動量の保存則を表わしている。(関連項目 福済寺の床)
左図のように、ストーンが溝のなかを、中心に向かって滑れば、ストーンはコリオリの力のため、右に曲がろうとして溝の壁を回転と同じ向きに押すので、リンクの回転は速くなると考えられよう。また、逆に、中心から遠ざかるように滑らせると、ストーンは溝の壁を、リンクの回転と逆向きに押すので、リンクの回転は遅くなるだろう。つまり、ストーンが中心に近づけば、リンクの回転は速く、遠ざかれば遅くなる。これは角運動量の保存則を表わしている。(関連項目 福済寺の床)
回転リンク上のカーリング
 回転運動
回転運動
コメント