コリオリの力
満天に星降る夜、僕は赤道直下の大地を北へ向かって歩いていた。やがて、地平線から北極星が昇り、それを中心として、プラネタリウムの中のように、星座がゆっくりと、左まわりに回転していた。
いつのまにか、僕は得体の知れない力を感じるようになっていた。その力は、僕が移動するたびに右方向に働き、立ち止まるとなぜか消えた。
北極星の高度が上がるにつれ、その力は強くなり、僕は東のほうに倒されそうになるのを我慢して、しっかりと大地を踏みしめながら、ひたすら北へ向かって歩いた。
僕は星座の回転が次第に速くなっていることを発見した。不思議な力と関係しているのだろうか。北極星は揺らめく薄いグリーンのカーテンの間に見え隠れしながら、既に頭上近くにまで昇っていた。
僕は氷原に立っていた。星座は天頂のまわりに回転していた。北極星の真下まで来たようだ。僕は、今、地球の自転軸の上に立っているのだ。
僕が両腕を水平方向に伸縮させると、星座の回転速度が変化するのが分かった。例の不思議な力が今度は僕の腕に働いているに違いない。
両手を縮めると、星座の回転が速くなった。腕に働く不思議な力が僕の体を星座の回転と逆向きに、つまり、地球の自転と同じ向きにねじるためだろうか。
今度は北極から赤道に向かって歩いてみた。すると不思議な力は西向きに働き、前とは逆に、星座の回転が遅くなるのが分かった。不思議な力は進行方向に対していつも右方向に働くようだ。
星座の回転速度が変化するのは、不思議な力が僕の足を通して地球の自転速度を変えているからに違いない。
次に北半球を東西方向に歩いてみた。不思議な力はやはり進行方向に対して右向きに働いた。しかし、北極星の位置がいくらか揺らいだように思えたが、今度は星座の回転速度に変化はなかった。
いずれにしろ、不思議な力は進行方向に対していつも右方向に働き、僕が北極に立てば、地球の自転は速くなり、赤道に立てば遅くなるのだ!
福済寺のフーコーの振り子を見た日の夜、僕は不思議な夢を見た。巨人になって、北半球の夜の荒野をさ迷い歩いていた。
僕が夢に見た不思議な力の正体は、コリオリの力と呼ばれる地球の自転による見かけの力だったようである。そして、巨人になった僕に働くコリオリの力が地球の自転速度を変えていたのである。
フーコーの振り子
現在では周辺の高層ビルの陰に隠れてしまったが、かつては、長崎駅に降り立ち、正面、山手のほうを見ると、亀の背中に乗った慈母観音が、右手に甘露の壺を持ち、左手で印を結び、観光客を出迎えてくれていた。黄檗宗の禅寺、福済寺であるが、この寺の堂には日本で一番長いフーコーの振り子が揺れている。
 観光案内によれば、かつて国宝であった福済寺は原爆で破壊されたが、現在の建物が新しく建立された際、地球の平和が、その自転のように、いつまでも続くことを願って、フーコーの振り子が作られたとのことである。長崎に原爆が落ちた時間、11時02分になると、毎日、福済寺の鐘が鳴らされる。
観光案内によれば、かつて国宝であった福済寺は原爆で破壊されたが、現在の建物が新しく建立された際、地球の平和が、その自転のように、いつまでも続くことを願って、フーコーの振り子が作られたとのことである。長崎に原爆が落ちた時間、11時02分になると、毎日、福済寺の鐘が鳴らされる。
振り子とお寺とは面白い取り合せだが、世界最初のフーコーの振り子が取り付けられたのも寺院であった。1851年、フランスの実験家フーコー は、寺院の礼拝堂の天井から長い振り子を釣り下げて長時間振らすと、振り子の振動面が変化することを示した。このことから、地球が自転していることを実証してみせたのである。
振り子を長時間振らせ続けるためには、空気の抵抗が小さくなるように振り子の速度を遅くし、さらに振り子の運動エネルギーを大きくする必要がある。福済寺の振り子は長さ25mの針金で金属球を吊るしたものであり、約10秒の周期で振れている。振り子の支点には摩擦を小さくするため、ダブルナイフエッジが使用されている。
フーコーの振り子を北極点で振らせると、そこでは地球表面が、一日の間に、上から見て左まわり(反時計まわり)に一回転しているから、地球表面に立って見れば、振り子の振動面は、一日に360度だけ右回りに回転しているように見えるはずである。
南極点では振り子の振動面は逆に左まわりに1回転する。また、赤道上では振り子の振動面は回転しないことは明らかであろう。それなら、中緯度に位置する福済寺では、振り子の振動面は一日にどのくらい変化するだろうか。
床の運動
地球の自転軸が北極星を指しているので、地球が完全な球であれば、福済寺の緯度をΦ とすると、そこから、北を向いて、仰角 Φで見上げた方向に北極星がいつも見えることになる。
フーコーの振り子の振動面の変化を知るために、福済寺の床面が、地球の自転のため、どのような運動をしているかを考えてみよう。
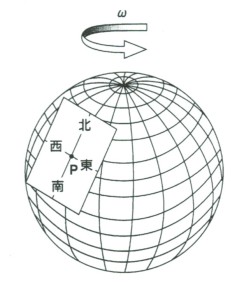 福済寺の床面は、左図のように、北緯 Φの地点で地球面に接しながら、地球の自転軸のまわりを、地球自転と同じ角速度ωで回転していることになる。
福済寺の床面は、左図のように、北緯 Φの地点で地球面に接しながら、地球の自転軸のまわりを、地球自転と同じ角速度ωで回転していることになる。
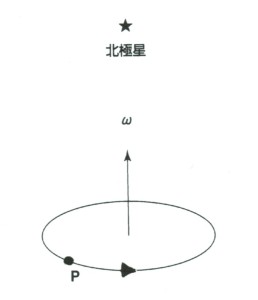
福済寺の床面に東西南北の方向を書き込んだとしよう。慣性系から福済寺の床面をみれば、地球の自転のため、床の中心Pが自転軸のまわりに円運動するとともに、床面に書き込んだ東西南北の向きが慣性系に対して変化している。
床面の運動は、微小時間の間なら、P点の並進円運動とP点の周りの回転運動に分解することができる。P点の並進円運動とは、床の平面の向きを一定に保ったまま、P点が地軸のまわりに円運動をすることである。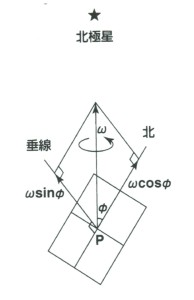
一方、後者の回転運動とは、P点を固定して、北極星の方向を回転軸として、床面が角速度ωで回転することである。
回転もベクトルであるので、床面のこの回転はさらに二つの回転に分解される。一つは床面上に書き込まれた南北軸のまわりの回転で、もう一つは床面に垂直な軸のまわりの回転である。結局、福済寺の床面の運動は、次のような、①~③の三つの運動に分解することができる。
①地軸の周りの並進円運動 (角速度:ω )
②南北軸のまわりの回転運動(角速度:ωcosΦ )
③床に垂直な軸のまわりの回転運動(角速度:ωsinΦ )
北極では①と②は存在せず、③の回転のみが存在し、その角速度の大きさはωである。また、赤道上では③は存在せず、①の並進円運動と南北の周りの角速度ωの回転運動②が存在する。中緯度にある福済寺の床は、重りの真下の点が円運動をするとともに、南北軸の周りの回転と垂直軸の周りの回転が混じった運動をしている。
みかけの力
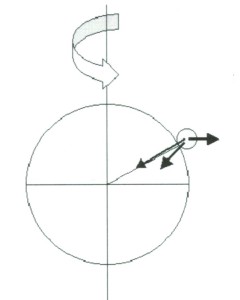 床の並進円運動①は、質量 の物体に遠心力を及ぼす。物体が地表に対して運動しているか否かにかかわらず、地上の物体に働くこの遠心力のため、重力は補正され、その方向が地球の中心方向からずれるとともに、補正された重力加速度の値は低緯度の場所ほど小さい値を示す。
床の並進円運動①は、質量 の物体に遠心力を及ぼす。物体が地表に対して運動しているか否かにかかわらず、地上の物体に働くこの遠心力のため、重力は補正され、その方向が地球の中心方向からずれるとともに、補正された重力加速度の値は低緯度の場所ほど小さい値を示す。
この遠心力の効果をとりいれると、赤道上での重力加速度の大きさは極地より、0.03ms-2 程小さいことになるが、さらに、地球が完全な球でない効果が加わるため、赤道での重力加速度の大きさは0.05ms-2 程度極地より小さくなる。
なお、重力加速度の大きさは陸上と海上とでも違いがある。アイソスタシー(地殻均衡論)によれば、氷山が水の上に浮いているように、地殻はそれより密度の大きいマントルの上に浮かんでいると考えられ、陸上物質より海底物質の密度のほうが大きい。そのため、一般に、海上の重力加速度のほうが陸上より大きくなる。
②で表わされる床面の回転は、地上で垂直に落下する物体の軌道に東向きの見かけの力を及ぼす。つまり垂直方向の運動に対するコリオリの力であり、落下方向は鉛直下方からずれてくる。この場合、床面の回転と一緒に重力の向きも変化するので、地表から見た落下方向のずれを直感的に求めるのは難しいが、自由落下の軌跡は鉛直線とならず、落下距離の1.5乗に比例して鉛直線から東にずれていく。
この曲線はナイルの曲線と呼ばれているが、もし、東京タワーのてっぺん333mの高さから物を落下させれば、落下点は10cmほど鉛直真下から東にずれる計算になる。鉛直方向の運動に与えるこの効果は赤道上で最大となる。
床の回転③は地上を水平方向に運動する物体に対してコリオリの力を及ぼすことになる。これが夢の中の僕に働いた不思議な力であり、また、フーコーの振り子の振動面を変化させる力である。
コリオリの力は、北半球では、進行方向に対して、右方向に働き、南半球では左方向であるが、ともにその大きさは両極で最大となる。
長崎の緯度は約33°であるので、福済寺の床面はその垂直軸のまわりに一日に196度ほど、上から見て左回転している。これを床面上の観測者から見れば振り子の振動面が同じだけ逆方向に回転して見えることになる。
前方の目標物に向かって物を投げると、投げる方向に関係なく、物が目標物に到達する間に目標物は地面の回転のため北半球では左にずれる。これを地面に立ってみれば、投げられた物が右カーブしているように見える。
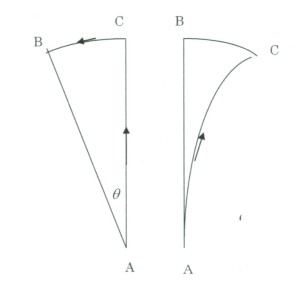 緯度がΦの北半球で、水平方向に一定の速さvで運動している質点に働くコリオリの力を求めてみよう。左側の図のように、地表上の点Aから距離 sだけ離れた点Bに向かって時刻t=0に 質量 mの弾丸を速さv で水平に発射したとする。
緯度がΦの北半球で、水平方向に一定の速さvで運動している質点に働くコリオリの力を求めてみよう。左側の図のように、地表上の点Aから距離 sだけ離れた点Bに向かって時刻t=0に 質量 mの弾丸を速さv で水平に発射したとする。
地球が自転していなければ、時刻 t=s/vに弾丸は点Bに達するはずであるが、地面が角速度 で反時計回りに回転しているので、発射して時間 t後には、点Bは弾道に対して角度 θ=ωtsinΦだけ回転している。つまり、点Bは弾道上から左に距離 sθだけずれていて、弾丸はB点より右にsθ離れたC点を通過する。
これを地表からみれば、右図のように弾道が直線から右ずれながらC点に向かうように見える。弧BCの長さをLとすればL=sθ=ωvt2sinΦとなる。L を時間 で2回微分すれば、右にずれていく加速度は2ωvsinΦ となる。これは弾丸にその進行方向に対して右向きに見かけの力 2mωvsinΦが働いていることになる。この見かけの力がコリオリの力である。
太平洋や大西洋の地球規模の海流は北半球では流れに対して右向きのコリオリの力を受けるため、一般に、海流は北半球では右回りであり、南半球では左まわりとなる。これに対して低気圧の渦は北半球では左巻き、南半球では右巻きであり、海流とは逆であるが、これもコリオリの力のためである。
空気は低気圧の中心に向かって吹き込もうとするが、コリオリの力のため、風向きが右方向にずれようとする。そのため、風は常に左に方向修正しながら吹き込むため左回りになる。
一方、これを慣性系から見れば、空気は低気圧の中心に向かって吹き込もうとするが、地球の自転と一緒に、気圧の中心は左へ左へと移動し、風はそれを追いかけて吹き込むため、風は左巻きに吹き込むと説明することもできよう。高気圧からは北半球では海流と同じくコリオリの力のため右回りに風が噴き出す。
変形する回転体
夢に見た巨人の話を定性的に考えてみよう。その場合、巨人の存在によって地球の軸対称性が破れ、自転軸の向きも変化することになるが、複数の巨人を考えることによって、地球と巨人からなる系の軸対称性は保存されると考えよう。つまり、巨人が動いても、自転の角速度が変わるだけで自転軸の向きは変わらないとしよう。
巨人が、北極点で両手を屈伸させると、腕に働くコリオリの力によって、巨人はねじられ、地球の自転速度が変化すると考えられるが、氷上のスケーターもスピンの速さを変えるのに腕を屈伸させる。スケーターが腕を縮めると、回転は速くなり、伸ばすと遅くなる。地球と巨人からなる系も同様に、質量が回転軸に近づくと回転の角速度は増し、質量が回転軸から遠ざかると角速度が減少する。
 ここで、回転体の慣性モーメントという量を考えよう。慣性モーメントは回転体の質量のみならず、その形状に依存する量である。例えば、左の写真の二つの独楽の質量はほぼ等しいが、慣性モーメントはAのほうがBより大きくなる。
ここで、回転体の慣性モーメントという量を考えよう。慣性モーメントは回転体の質量のみならず、その形状に依存する量である。例えば、左の写真の二つの独楽の質量はほぼ等しいが、慣性モーメントはAのほうがBより大きくなる。
慣性モーメントとは、回転体の質量が同じなら、質量が回転軸から遠くに分布しているほど大きくなる量である。巨人の話では、巨人が赤道にいる時、地球と巨人からなる系の慣性モーメントは大きく、地球の自転の角速度は小さい。
巨人が北極に近づくと、全体の質量は変わらないが、系の慣性モーメントは小さくなり、そのため自転の角速度は大きくなる。これはアイススケーターがスピンをする場合、スケーターが腕を縮め、体の慣性モーメントを小さくすると、回転が速くなるのと同じである。
慣性モーメントと角速度の積を角運動量という。外力がなく、回転体が内力だけで変形しながら回転しているとき、角運動量は保存する。ただし、変形の途中でも角運動量は定義できるが、物体の角速度は厳密には定義できない。変形の途中では物体の各部で角速度が異なるからである。
外力が働いていなければ、変形しても角運動量は保存するため、変形の前後で、角速度が変化する。地球と巨人からなる系で、巨人が自転軸上にくると、自転が速くなるのは、系の慣性モーメントが小さくなるため、角運動量の保存則から、自転の角速度が増したと考えることもできる。
巨人がどこに居ても系の角運動量は変わらないが、系の自転のエネルギーは巨人が極点に近づくほど大きくなる。エネルギーのその増し高は自転の遠心力に逆らって巨人がした仕事である。つまり、地表面を歩く巨人に働く重力は、地表面に完全に垂直でないため、巨人は地軸に近づくときは仕事をしなければならなくなるのである。
最近、地球温暖化による海面の上昇が問題となっているが、仮に南極の氷がすべて解けたとすると、世界中の海面が60mほど上昇すると言われている。氷が解け、赤道に向かう流れにはコリオリの力が働き、摩擦をとおして、地球の自転は遅くなる。海面が60m上昇すれば、地球の慣性モーメントが割合として10-5ほど増えるので、角運動量保存則から地球の角速度も同じ割合だけ遅くなり、地球の自転エネルギーも10-5だけ小さくなる。損失分は海水の摩擦によって、熱エネルギーとして消失することになるが、その量は1024ジュールとなる。これは地球の自転が潮汐摩擦のために1万年間に失うエネルギーに相当する。
回転椅子の実験
回転座標系での見かけの力として遠心力とコリオリの力があるが、遠心力は車がカーブするときなど、体験できる機会が多いのに対し、日常の生活のなかで、コリオリの力を体験する機会はほとんどない。しかし、回転椅子を用いるとコリオリの力が簡単に体験できる。
 回転椅子に座り、鉄アレイを持った両手を広げ、回転椅子を回転させると、鉄アレイには遠心力が働く。そして、この状態で手を縮めると、鉄アレイには、さらにコリオリの力が働き、体が回転方向にねじられ、回転が速くなる。
回転椅子に座り、鉄アレイを持った両手を広げ、回転椅子を回転させると、鉄アレイには遠心力が働く。そして、この状態で手を縮めると、鉄アレイには、さらにコリオリの力が働き、体が回転方向にねじられ、回転が速くなる。
見方を変えれば、腕を縮めると、鉄アレイも含めて人全体の慣性モーメントが小さくなるので、回転が速くなるのであり、角運動量保存則でもある。このとき、角運動量は一定であるが、腕を縮める際、遠心力に逆らって仕事をするので、回転のエネルギーは増すことになる。
次に片腕で鉄アレイを持ち、回転椅子に座り、回転椅子が静止した状態から、鉄アレイを持った腕を水平面内で円を描くように回すと、椅子が鉄アレイの回転と逆向きに回転し、体の向きを変えることができる。最初に全体の角運動量はゼロであったので、鉄アレイを回転させている間も全角運動量はゼロでなければならない。そのため、鉄アレイに生じた角運動量を打ち消すように椅子が回転する。鉄アレイの回転を止めると椅子の回転も止むが、椅子の向きは最初と異なっている。
惑星の運動の角速度は遠日点では遅く近日点では速くなる。これは角運動量の保存則を表わすケプラーの第2法則を用いれば明らかであるが、これも回転椅子の実験と同じく、コリオリの力からも定性的に導かれる。
惑星の角速度と一緒に回転する座標系から惑星の運動を見ると、惑星の運動は動径方向のみとなる。惑星が太陽から遠ざかるときは、コリオリの力は惑星の公転方向と逆方向に働くので、惑星の角速度、すなわち、座標系の角速度も小さくなる。逆に太陽に近づくときは回転が速くなることが直感的に理解できよう。
星の収縮
星間物質が収縮して星が生まれるとき、あるいは星が収縮して高密度の星になるとき、星の回転速度は増す。この場合にも物質が中心に向かうとき、コリオリの力が働き、回転速度が増していると考えることもできるが、星の慣性モーメントが小さくなるため、角速度が増すと考えることもできる。
星が収縮する場合は星全体の力学的エネルギーが減少するため、その分、星は発熱する。収縮することによって解放された重力エネルギーの半分が星の回転エネルギーを増加させるために使われ、残りの半分は熱エネルギーとなって星の内部温度を上げ核融合を引起こす。
中性子星がまわりの物質を取り込む場合であれば、コリオリの力は中性子星の周囲に降着円盤を形成させ、解放された残りの重力エネルギーは降着円盤の温度を数億度にまで上昇させ、その温度に相当する黒体輻射の光、つまりX線を放出させることになる。(関連項目 回転リンク上のカーリング)
福済寺の床
 回転運動
回転運動
コメント
パリティ(丸善)2000年1月号に投稿したものに加筆したものです。
http://ci.nii.ac.jp/naid/40004595599