衛星と惑星のはざまで
万有引力の法則によれば、二つの天体の間に働く引力は、天体間の距離の2乗に反比例し、二天体の質量の積に比例する。月に働く太陽と地球の引力を比較してみよう。月から太陽までの距離は、地球の公転半径とほぼ同じであるから、1天文単位、つまり、約1億5千万kmであり、これは、月から地球までの距離38万kmの約400倍である。一方、質量に関しては、太陽は地球の約33万倍である。これから月に働く太陽と地球の引力の比を求めると、太陽の引力は地球の引力のほぼ2倍となる。
大岡政談では、こどもの母親だと主張して譲らぬ二人の女性に、こどもの左右の手を両方からそれぞれ引っ張らせ、勝ったほうでなく、負けたほうを本当の母親だとして裁定を下したが、太陽は、地球の倍の力で月を引っ張るのに、月は地球から剥ぎ取られ惑星になることなく、地球の衛星のままでいられるのも、自然法則のなせる「大岡裁き」であろうか。
円制限三体問題
太陽と地球と月のように、三つの天体からなる系の運動を三体問題とよぶ。男女の三角関係のように、三体問題も複雑であり、一般に解析的には解けず、その運動は数値計算で解くしかない。三体問題のうち、第三の天体の質量が第一、第二の天体に比べ充分小さい場合を制限三体問題という。この場合、第三の天体は、第一および第二の両方の天体の運動の影響を受けるが、逆に第三の天体の運動が第一および第二の天体に影響を及ぼすことはないものとする。第一と第二の天体の運動は二体問題であるから解析的に解けるので、その二つの天体によってつくられた重力場の中を第三の天体が運動することになる。
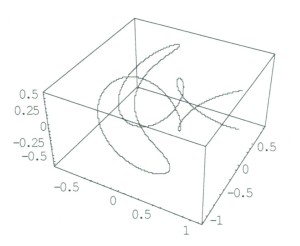
さらに、第一、第二の天体が等距離を保って運動している場合、円制限三体問題という。しかし、この場合にも、第三の天体の運動は解析的には解けない。図1は円制限三体問題での小天体の軌道を計算ソフトで数値計算した結果である。
円制限三体問題では、系の重心を中心とし、第一第二の運動と同じ角速度で回転する回転座標系上で考えれば、第一第二の天体の位置は固定されるので、第3の天体のみが回転座標系上を運動することになる。しかし、この場合、第三の天体は、第一および第二の天体からの引力に他に、遠心力とコリオリの力を受けながら回転座標系上を運動することになる。
第三の天体、つまり、小天体の運動は、一般にはカオスになり、図1のような複雑な軌道を運動するが、この場合、第一、第二の天体を固定した回転座標系から見たとき、ラグランジュ・ポイントと呼ばれる力の働かない場所が存在する。
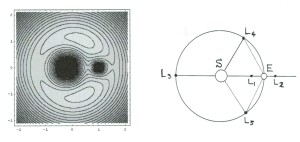
回転座標系上を運動する小天体には次の四つの力が作用する。①地球の引力、②太陽の引力、③座標系の回転による遠心力、そして、④コリオリの力である。このうち、④のコリオリの力は小天体が回転座標系に対して静止していれば働かない。つまり、ラグランジュ・ポイントとは①②③の三つの力が釣り合う点である。①と②には、それぞれポテンシャルが存在し、保存力であり、③についても遠心力ポテンシャルが存在するので、小天体は①②③の三つの力の和で表される保存場のなかを、コリオリの力を受けながら運動していることになる。
三つの力の和が釣り合う場所は、図2の右図のように、L1 ~L5 までの五箇所が存在する。これらのラグランジュ・ポイントのうち、L1~L3 はラグランジェの直線解とよび、 L4とL5 はラグランジェの正三角形解と呼ばれる。L4 とL5 がそのように呼ばれる所以は、それらが地球の公転軌道上にあり、太陽と地球と正三角形をなす位置に存在するからである。
ラグランジェ・ポイント
図2の左図は有効ポテンシャルを計算ソフトで計算した結果である。直線解L1、L2、L3では有効ポテンシャルが鞍点になっているが、正三角形解L4、L5では極大点になっている。但し、ポテンシャルの等高線が分かりやすいように、計算では地球の質量を太陽に質量の0.2倍としている。実際には、地球の質量は太陽の 3×10-6 倍である。
地球の引力①が小天体を地球の近くに留めておこうとするする力であるのに対し、太陽の引力②と遠心力③の和は、地球近傍では、小天体を地球から引き離そうとする太陽の起潮力である。地球の中心での遠心力は太陽の引力と釣り合っているので、そこでは、②と③の和は0、つまり、太陽の起潮力は地球の中心ではゼロである。
小天体の位置が地球の中心から太陽側に離れると、太陽の引力が遠心力よりも強くなるので、起潮力は太陽のほうを向き、地球から遠ざかるほど強くなり、地球の引力は弱くなるので、地球と太陽を結ぶ線上に、太陽の起潮力と地球の引力とが釣り合う場所が存在する。これがL1点である。同様にして、地球に関してL1と反対側にも釣り合いの点L2が存在する。L1もL2も太陽の起潮力と地球の引力が釣り合う場所であり、それよりも地球に近い点では地球の引力が太陽の起潮力に勝るのである。
L1やL2は地球から150万km離れているのに対し、月までの距離は38万kmであるから、月は二つのラグランジュ・ポイントの内側を回っているので、地球の惑星でいておれるのである。大岡裁きで地球の引力と比べるべきは、太陽の引力ではなく、太陽の起潮力だったのである。
ラグランジェ・ポイントの安定性
ラグランジェ・ポイントは、しばしば、スペースコロニーを安定させる場所としてSFにも登場するが、力の平衡点がすべて安定な平衡点とは限らない。ラグランジェ・ポイントの位置に小物体を安定させることはできるだろうか。
二つの天体からの万有引力のポテンシャルと遠心力ポテンシャルの和を有効ポテンシャルと呼ぼう。力の平衡点が有効ポテンシャルの窪みになっていれば、そこに小物体を安定させることができるが、直線解はいずれも有効ポテンシャルのサドル・ポイントであり、正三角形解は有効ポテンシャルの極大点となっている。
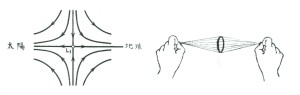
直線解の場所では、小天体は地球の引力と太陽の起潮力によって両側に引っ張られている。そのため、直線解のまわりには、それぞれ、地球の公転軌道面と直交する準安定の立体軌道が存在するが、その近傍の力の模式図および立体軌道のモデルは図3のように表すことができよう。立体軌道モデルの左右の糸の張力は太陽の起潮力と地球の引力に相当する。
図4もMATHEMATICAでの計算結果である。L1点のまわりの立体軌道であるが、L1もL2もそのまわりの立体軌道はいずれも安定でなく、準安定であるため、そこに投入された小物体は軌道修正をしなければ、長期間そこにとどまることはできない。
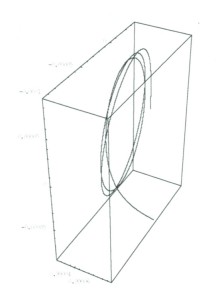
計算結果でも、立体軌道は軌道修正をしなければ、小物体は数回まわったあと、急激にL1点から離れていく。
直線解に対し、正三角形解の近傍では、そこに投入された小物体はさらに奇妙な振る舞いを見せる。そこは有効ポテンシャルの極大点になっているので、小物体の位置がそこから少しでもずれれば、小物体はポテンシャルの坂を滑り落ちるように思えるが、面白いことに、コリオリの力のため、小物体は極大点の周りに安定に留まることができる。
ラグランジュの正三角形解では、遠心力と地球および太陽からの引力が打ち消されるので、それらの点の近傍では、小天体に働く力は、ほぼ、コリオリの力のみとなる。正三角形解の近傍の小物体は、いくら追い払っても寄ってくるパパラッチかストーカーのように、ポテンシャルの極大点から僅かながらも斥力を受けるにもかかわらず、その点に纏わりつき、その近傍に安定に留まるのである。
太陽と地球の系の場合、L4 やL5 には、人口天体はもとより、天然の天体も存在していないようである。しかし、ラグランジェ・ポイントは太陽と木星の系にも存在し、その場合、正三角形解に相当する二箇所の位置には、トロヤ群と呼ばれる小惑星群が存在している。木星の軌道上を前後に分かれて運行するトロヤ群の名前の由来は、天空神ジュピター(木星)の子孫が、ギリシャ軍とトロイ軍に分かれて戦ったトロイ戦争にちなんだものであり、トロヤ群の中の小惑星にはアキレウスやヘクトルなどトロイ戦争の勇者の名がつけられている。
月の運命
現在、地球から38万㎞の距離にある月は、潮汐摩擦によって地球の自転から角運動量とエネルギーをもらいながら、僅かずつ地球から遠ざかっている。もし、将来、月がL1やL2 よりも遠ざかると、月は地球の衛星として留まることはできず、太陽系のなかを彷徨うことになろう。しかし、月が遠ざかるのは、潮汐摩擦によって失われた地球の自転の角運動量の分だけ、月の公転の角運動量が増えるからである。月が地球から60万㎞程度まで離れると、地球の自転の角速度と月の公転の角速度が等しくなり、地球も月に同じ面を向けることになるので、そうなれば潮汐摩擦はなくなり、月までの距離の変化も止むので、将来も月は地球の衛星のままでいられそうである。
源氏物語宇治十帖
数々の女性と浮名を流した光源氏の死後、源氏物語には互いにライバルと目する二人の公達が登場してくる。光源氏の子として育てられたが、実は、光源氏の晩年に、妻の不義密通によって生まれた子、薫と、光源氏の孫で、その女好きの血筋を引く匂宮である。
「いずれの御時にか」で始まった五十四帖からなる長編小説も、宇治十帖とも呼ばれる最後の十帖で終盤を迎え、そこでは光源氏ゆかりの二人の公達と彼らを取り巻く女性たちの物語が展開する。源氏物語最後のヒロインとなる浮舟は、二人の男性、薫と匂宮との愛のはざまで、波間に漂う小舟のように苦悩し、その三角関係を清算するため死を決意し入水するも僧都(そうず)に助けられて出家する。
万葉集にも、複数の男性に求婚された真間の手児奈(ままのてこな)や菟原処女(うないおとめ)のように、美しさゆえに悲劇のヒロインとなった女性が詠われている。彼女らは最後には死を選ぶのだが、昔も今も光源氏のように女漁りに明け暮れたドンファンはいるのに、言い寄る男たちを手玉に取り、したたかに生きぬいた女性は昔はいなかったのだろうか。
明けくれに昔こひしきこころもて 生くる世もはたゆめのうきはし
後年、源氏物語を現代語訳(源氏物語礼讃)し、紫式部を終生の師と仰いだ与謝野晶子が詠んだ歌である。明けても暮れても、昔のことが恋しく思い出されながら生きていく人の世も、もしかしたら、夢の浮橋のように儚いものだろうか。
源氏物語の最終章である五十四帖「夢の浮橋」は、薫が、助かった浮舟の居場所を人づてに探しあてたところから始まる。薫は浮舟に文を送り、また人を遣わすが、浮舟は人違いだとして面会をかたくなに拒む。薫は、第三の新たな男が現れ、その男が浮舟を引き留めているのではないかと思い、あきらめて去っていく。
男女の色恋沙汰を描いた王朝文学の最高傑作は、この五十四帖で長い幕を閉じる。浮舟が最終的に辿り着いたのは、薫でも、匂宮でもなく、また他の男でもなく、仏門だったのだが、アメリカのNASAは源氏物語から遥か千年の時を経た今、最後のヒロインを現代の宇宙工学のなかに甦らせたようである。
愛憎渦巻く俗世から離れ、その後は一転して心静かな余生を送ったであろう浮舟のように、宇宙にも、衛星にしようとする地球の引力も、惑星にしようとする太陽からの起潮力をも、頑なに拒絶するかのように、何もない一点の周りに、仏の光輪にも似た、ハロー軌道と呼ばれる奇妙な軌道を描いている複数の人工天体が存在している。
地球の軌道の中心には太陽があり、月の軌道の中心には地球があるように、天体が閉じた軌道上を運動するとき、その中心には、一般に引力源の別の天体が存在している。しかし、ハロー軌道の中心に、引力源となる天体はなく、しかも、その軌道面は地球のほうを向き、地球の公転面とほぼ直交している。
現在、L1 点とL2 点のハロー軌道には観測用の人工天体が打ち上げられ、軌道修正をしながら、それぞれの点の周りを180日程度の周期で回っている。NASAのSOHOはL1 点のまわりを回りながら太陽活動を調査している。また、地球の影になり太陽の光に邪魔されないL2 点では、同じくNASAのマイクロ波観測衛星WMAPが、マイクロ波の宇宙背景輻射を観測し、宇宙の起源を解き明かす手がかりとなる情報を地球に送り続けているのである。
どうやらNASAの宇宙工学者達は双子の浮舟を造ったようである。姉妹の一人を年中、陽の光のなかに浮かし、対照的に、もう一人を、陽の当たらない、星空のなかに浮かしている。
参考:What is a Lagrange Point? | NASA Solar System Exploration

コメント
パリティ(丸善)2007年6月号に投稿した「衛星と惑星とのはざまで」に加筆訂正したものです。
http://jglobal.jst.go.jp/public/20090422/200902201672429312