球の表面積の公式を、微積分を知らない中学生でも導ける方法を考えてみた。
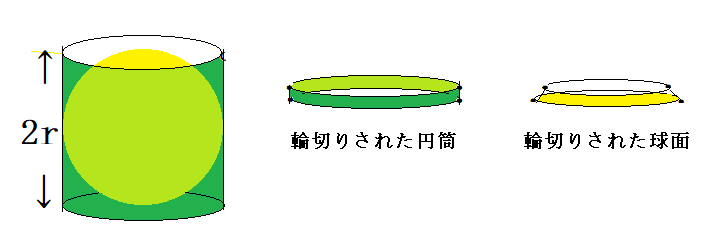
まず、図1のように、長さ2rの円筒のなかに接した半径rの球を考え、円筒と球を中心軸に垂直な面で薄く輪切りにしよう。具材として球形の卵の黄身の入っている海苔巻き寿司を輪切りする場面をイメージして頂きたい。
円筒と球面の両方が一緒に輪切りされるので、どの部分で切り取っても、輪切りされた円筒の薄片(青色)と球の薄片(黄色)の厚さは同じである。どこで切っても青の薄片の側面積は変わらないが、黄色の薄片では、どこできるかで半径も、表面帯の幅も変化する。しかし両者は反比例するので、黄色の薄片の側面積も一定である。つまり青と黄の両者の薄片の側面の面積はいつも等しくなる。
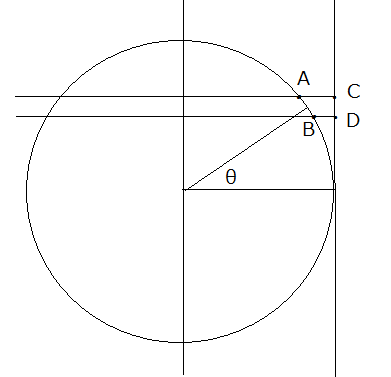
数式で示すと、図2において、球面上の点AとBを円筒上の点CとDに投影すると、CD=ABcosθであり、かたや、球の薄片の円周=円筒の薄片の円周×cosθであり、二つを帯状にすると両者の面積は等しくなる。幅は球の薄片の方が長いが、円周は円筒の方が長いので、図1の輪切りにされた二つの側面の面積はθに関係なく、円柱も球も2πr×CDに等しくなる。
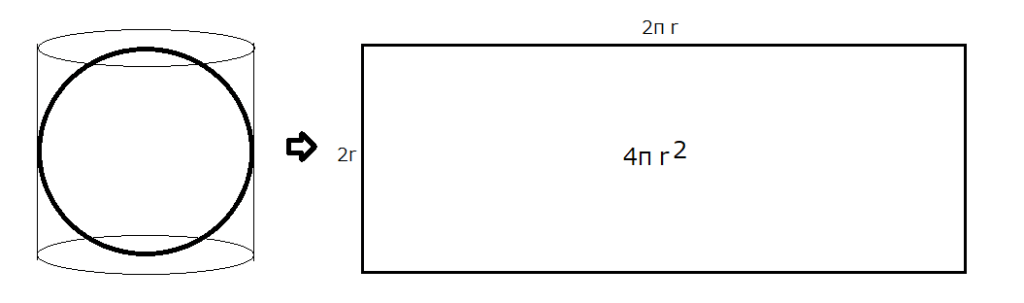
円筒と球の切り分けた二つの側面積が同じだから、全体も同じになる。球の表面積は、図3のように、円筒の側面積に等しくなり、4πr2 となることが分かる。
円柱と球を薄く切り分けて比較し、それを足し合わせるのだから、結局は微積分を使っているが、最初からそれをあからさまに表に出すと中学生は難しく感じる。生徒が微積分の問題だと気づかないうちに微積分の考えを教えることができよう。海苔巻き寿司輪切り法、転じて、中学生に微積分の考えをこっそり吹き込む方法である。
浮力の原理で知られるアルキメデスは、微積分が発見されていない時代に、球の表面積が大円の面積の4倍になることを知っていたと言われている。→ アルキメデスと球の表面積
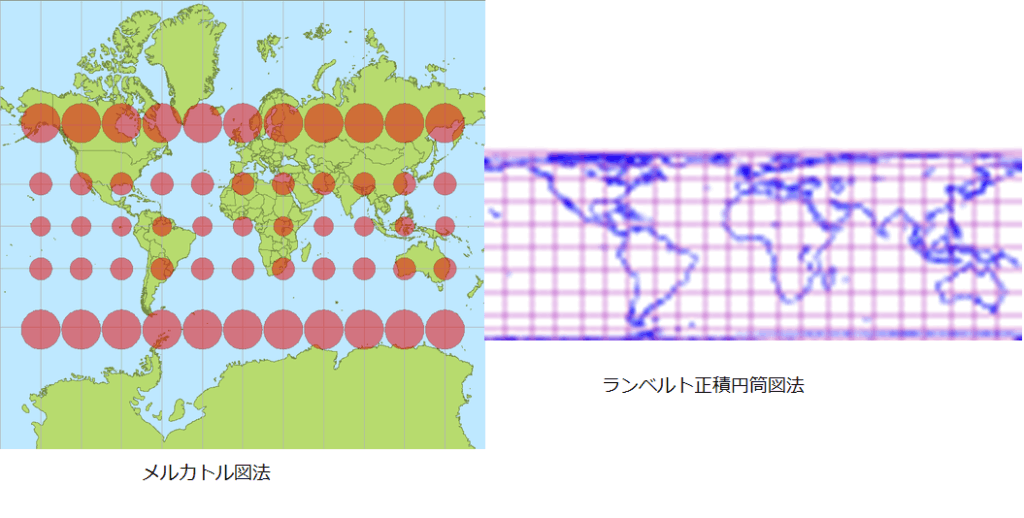
球の表面積を円筒に投射する図1あるいは図2の投影法は、現在、世界地図の作図法にも応用されている。世界地図にはいろいろな図法があるが、球面を平面に投影しなければならない。メルカトル図法で書かれた地図では、赤道上では縮尺どおりだが、高緯度では経度方向にも緯度方向にも同じ割合で引き伸ばされ、面積が拡大される。一方、図1や図2の巻き寿司法で作られた世界地図ランベルト正積円筒図法では、経度方向に引き伸ばされるのは同じだが緯度方向には逆に圧縮され、高緯度でも島の面積は変わらない。ただし、高緯度の島の形状は大きく変わる。
参考 メルカトル図法とランベルト正積円筒図法


コメント