満月から次の満月までの時間、つまり、月の満ち欠けの周期、朔望月は、月が地球の周りをまわる公転周期27.3日とは異なる。27.3日が無限遠方の恒星から見たときの周期であるのに対し、朔望月は、観測者が太陽の中心から、望遠鏡を常に地球に向くように自動追尾させながら地球と月の動画撮影をしたときの月の公転周期である。その動画では、地球の中心は画面の一点に静止し、月だけが往復運動をしている筈である。そのときの、月の往復運動周期が1朔望月の長さである。朔望月は太陽と地球が静止する回転座標系から見た月の公転周期になる。
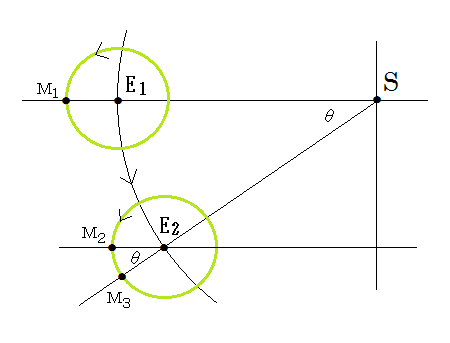
地球が太陽の周りを回る公転軌道も、月が地球の周りを回る公転軌道も、どちらも完全な円とし、二つの軌道面は一致しているとして、朔望月の長さを求めてみよう。図1は地球と月の運動を天の北極から見た図であり、地球も月も左まわりに公転する。太陽にいる観測者が、望遠鏡で地球と月を見たとき、両者が重なり、太陽、地球、月が、図1のS、E1 、M1のように一直線上に配置したとき満月であるが、望遠鏡の向きがθだけ変化し、つまり、地球が角度θだけ公転する間に、月が2π+θ回転すると、再度、S、E2、M3が一直線上に並び、再び満月となる。月の位置がM1からM2になるまでの期間が月の公転周期であり、M1からM3までになる期間が1朔望月の長さである。よつて、地球の公転の角速度をΩ、月の公転の角速度をωとすると、
θ/Ω=(2π+θ)/ω (1)
となる。ただし、πは円周率である。朔望月をT、地球の公転周期をTE、月の公転周期をTMとすると、T=θ/Ω、TE=2π/Ω、TM=2π/ωであるから(1)より、
1/T=1/TM-1/TE (2)
が成り立つ。TE=365日、TM=27.3日とすると、朔望月Tは約29.5日となる。
次に、小学生や中学生にも(2)式を導くことができるように、今度は天動説で考えてみよう。
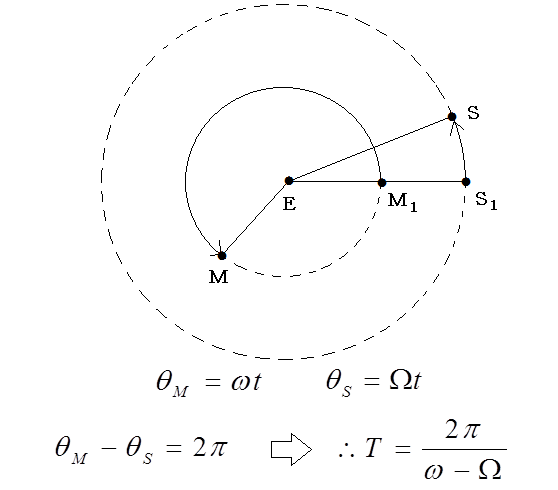
図2のように、天動説では地球を中心とする二つの同心円上を太陽と月とが、それぞれ、角速度Ωとωで運動することになる。太陽と月の公転面が一致していると仮定しているので、日食も月食も1朔望月ごとに起きる。新月には日食が起き、満月に月食になる。地球からみれば、新月の日に太陽と月とが重なるが、Ω<ωであるので、その後、単位時間が経過するごとに、太陽は、月に、角度ω-Ωずつが遅れながら地球の周りを公転する。太陽が一周遅れて、再び月と重なるまでの時刻は、2π/(ω-Ω)となり、それが1朔望月の長さTに等しくなる。そのことから(2)式が簡単に導かれる。地球を固定して考えれば、小学校で習う時計算の手法が使え、角速度Ωやωは一日あたりの回転角だから、Ω=360°/365日、ω=360°/27.3日、2π=360°として、丁寧に説明すれば、小学生にも理解できよう。天動説は天体の力学には使えないが、天体の幾何学だけを考えるときには地動説よりも簡単になる場合がある。
図1は太陽は動かず、地球が動く地動説であり、図2は地球が動かず、太陽が動く天動説であるが、地球と太陽を入れ替えて考えると、逆に、図2が地動説になり、静止した太陽の周りを惑星の地球と「惑星に変化した」月とがまわっていることになる。それに対し、図1は、「惑星に変化した」月が太陽の周りを回りながら太陽とともに、動かない地球の周りを回ることになる。これは天動説のほころびを繕うために考案された周転円の考えと同じになる。
参考:駅舎の時計

コメント