抗力説の利点―ブランコ―

　我が家では家計簿をつけていない。何度か家計簿用のノートは買ったものの長続きしない。最近はレシートをスマホで読み取るだけで家計簿をつけることができるそうだが、スマホを扱うこと自体面倒である。なにも、家計簿などつけなくても、収入は年金だけだから、通帳の残高だけを確認するどんぶり勘定のほうが、無精者の老夫婦には適している。支出の内訳が分からないので、医療費はいくらか、エンゲル係数はいくらかと聞かれても分からないが、家計簿をつけても　年金の額が増えることはないのだから、年金の範囲内で生活しているということだけがわかれば、それで充分であろう。　
　家計では、どんぶり勘定派の筆者だが、今回の力学の仕事を巡る筋力派との論争では、抗力説を唱え家計簿派にまわることになった。論争の内容については、これまでホームページでさんざん紹介してきたが、抗力説もエネルギーの出所は人の筋力だから、筋力説でも構わないではないかという考えもあろう。しかし、物理では、仕事の明細を考えたほうが、どんぶり勘定よりも遥かに分かり易く、しかも簡単である。抗力説の利点をブランコの運動を例にして紹介したい。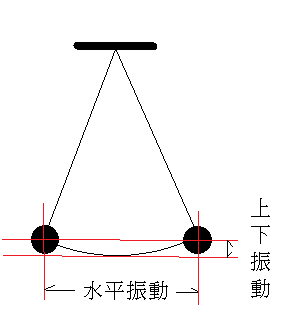
　上図のように単振子が振れているとき、重りの運動は水平振動と上下振動に分解して考えることができるが、外部から振り子の周期に合わせて外力を加えれば共振を起こすことができる。それには二つの方法がある。一つは水平方向に周期的な外力を加える方法であるが、これはブランコを一人では振れない幼児を母親が後ろから周期的な力を加えることに相当する。二番目の方法は、振り子の上下方向の振動に合わせて外力を加える方法であるがそれには少々工夫を要する。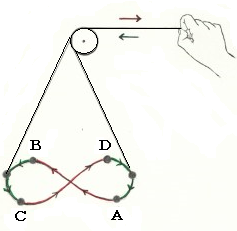
　スペインの教会にボタフメイロと呼ばれる大きな振り子がある。そのしくみは上図のように外力を加え振り子の長さを周期的に変化させているので重りは∞のような図形を描く。外力は重りが上に上がるとき引っ張り、振り子に正の仕事をし、下に下るとき力を緩め負の仕事をすることになるが、張力は引き上げるときが大きいので、振り子の1周期の間に張力は正の仕事をする。このときの仕事は張力と作用点の移動距離の積であるから、いわゆる仕事Bであり、その仕事量は振り子の全エネルギー（重りの運動エネルギーと位置エネルギーの和）の増分となる。
　この方法をブランコに応用し抗力説を適用すれば、ブランコの原理が簡単に理解できる。ブランコでは鎖の長さを変化させることはできないが、下図のように人がその筋力によって体を屈伸させ、その重心(赤い点）が∞図形を描くようにすれば、鎖の張力が重心運動に仕事をすることができる。但し、この時の仕事は張力と重心の移動距離との積であるから、いわゆる仕事Aである。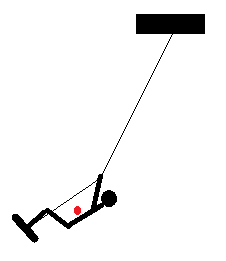　筋力が重心運動に直接仕事をすると考えると、内力が重心運動に仕事をすることになり、何が何だか分からなくなるが、二段階に分けて考え、筋力がまず変形運動に仕事をし、次に、抗力である張力が、変形運動と重心運動に正と負の仕事を同時にすると考えれば簡単である。ブランコはエネルギーを増すが、そのエネルギーの出所は人の筋力であることに変わりはない。筋力は変形運動に仕事をし、系にエネルギーを供給するが、重心運動に仕事をするのは抗力である。