相対的に等速直線運動する二つの慣性系KとK’のどちらから見ても、光の速度は同じでなければならない。そのためには、「光時計」の項で述べたように、座標系KとK’で時間の進み方が異なると考えざるをえない。
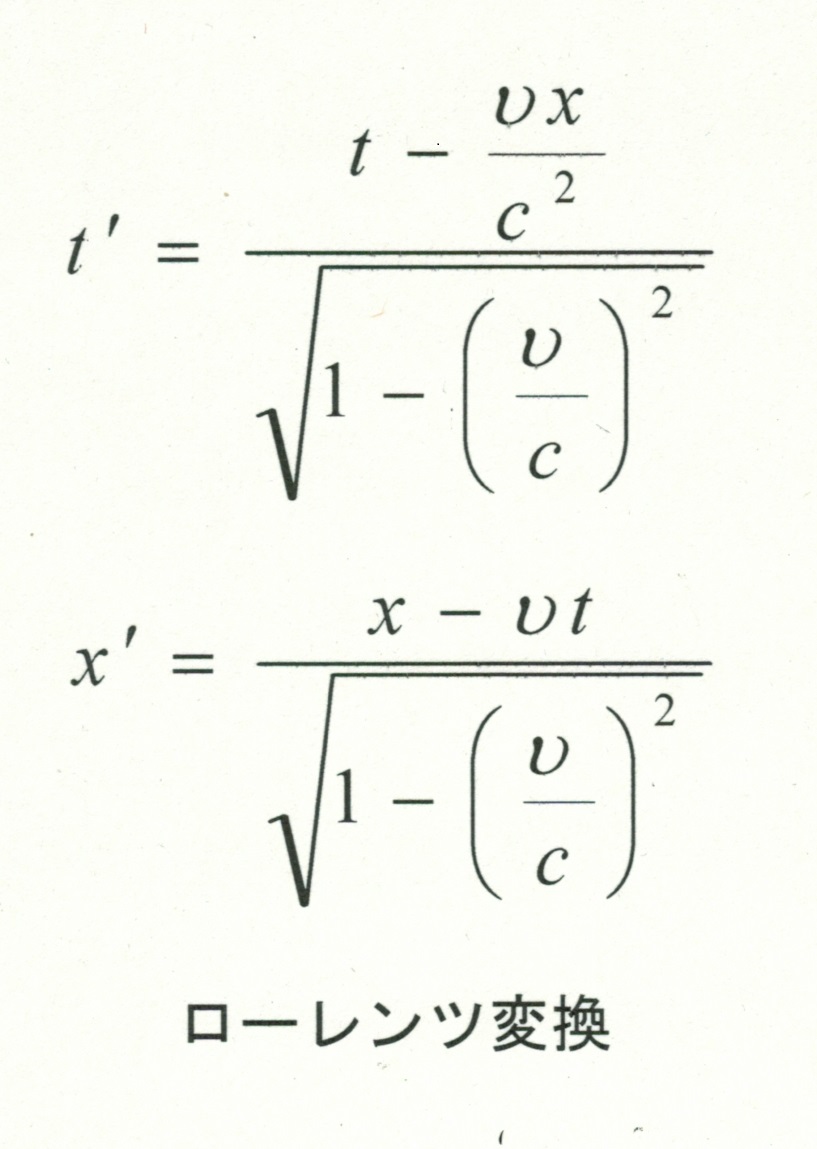 座標系Kに対して、座標系K’がxの正の方向に一定速度vで動いているとき、光速が一定であるためには、両者間の座標変換は、従来のガリレイ変換ではなく、左のようなローレンツ変換を採用しなければならない。y軸およびz軸は変わらないが、x軸と時間が二つの慣性系で異なる。ただし、両方の座標系の原点が重なった瞬間を時間の原点に選び、t=t’=0とする。
座標系Kに対して、座標系K’がxの正の方向に一定速度vで動いているとき、光速が一定であるためには、両者間の座標変換は、従来のガリレイ変換ではなく、左のようなローレンツ変換を採用しなければならない。y軸およびz軸は変わらないが、x軸と時間が二つの慣性系で異なる。ただし、両方の座標系の原点が重なった瞬間を時間の原点に選び、t=t’=0とする。
ローレンツ変換において、光速сを無限大にすると、t’=t、x’=x-vtとなり、ローレンツ変換はガリレイ変換に一致する。
座標系Kから見た光の角振動数をω、波数をk、つまり、波形をAsin(ωt-kx)とし、この光を座標系K’から見ればどうなるかを考えてみよう。ωt-kxにローレンツ変換を施した結果を、ω’t’-k’x’とすれば、簡単な計算から、
ω’/ k’=ω/k (1)
および、
ω’=((c-v)/(c+v))1/2ω (2)
が得られる。(1)式は二つの座標系で光速が等しいことを示している。ローレンツ変換はもともと光速が不変になるようにつくられているので、(1)が成り立つのは当然であるが、(2)はローレンツ変換に対して振動数が変化することを示し、光のドップラー効果を表している。ここでは、vは両者が離れていく速さを正としている。互いに近づく場合はvの符号を変えればよい。また、座標系Kでの波長をλ、K’での波長をλ’とすれば、
λ’=((c+v)/(c-v))1/2λ (3)
となる。
音のドップラー効果では、観測者に聞こえる振動数は音源の運動と観測者の運動の両方に依存するが、光のドップラー効果では、振動数や波長は光源と観測者の相対速度に依存する。
ローレンツ変換と光のドップラー効果
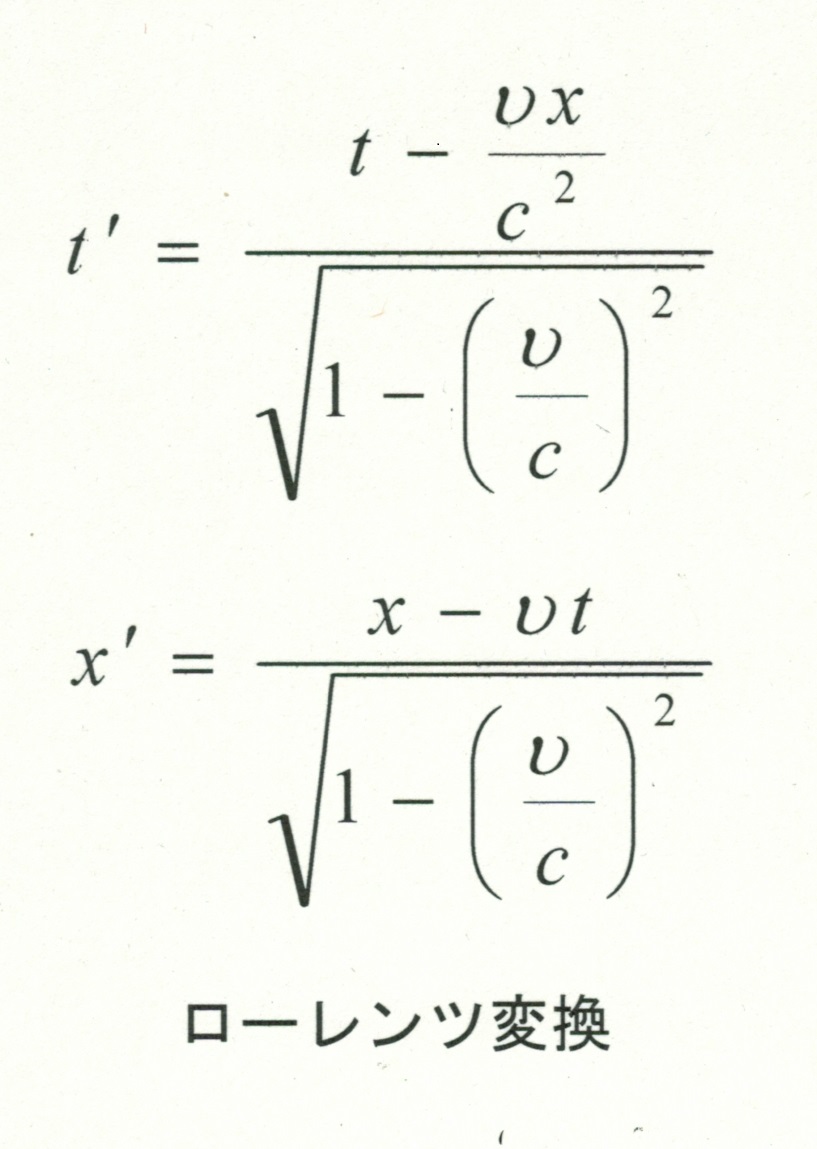 相対論
相対論
コメント