海水浴場の砂浜で休んでいると、斜め前方の海でこどもが溺れかけている。もはや、一刻の猶予もできない。こどもを助けるには、今いる場所から水際に向かって走り、そこから海に入り泳がなければならないが、砂浜を走る速さと泳ぐ速さは異なる。最短時間でこどものところに辿り着くには、水際のどの場所から海に入ればよいだろうか。これは光の屈折の問題と同じである。
フェルマーの原理によれば、任意の二点を結ぶ光路は所要時間が最小になるように決まる。光速が一定であれば、光は直進するが、水中の一点から水面上の一点へ、あるいはその逆の場合も同じであるが、異なる媒質の境界を跨いで進む光は境界面で屈折する。境界面での光の屈折の法則、つまり、スネルの法則は、所要時間が最小になるように光路を選ぶというフェルマーの原理からも導かれる。
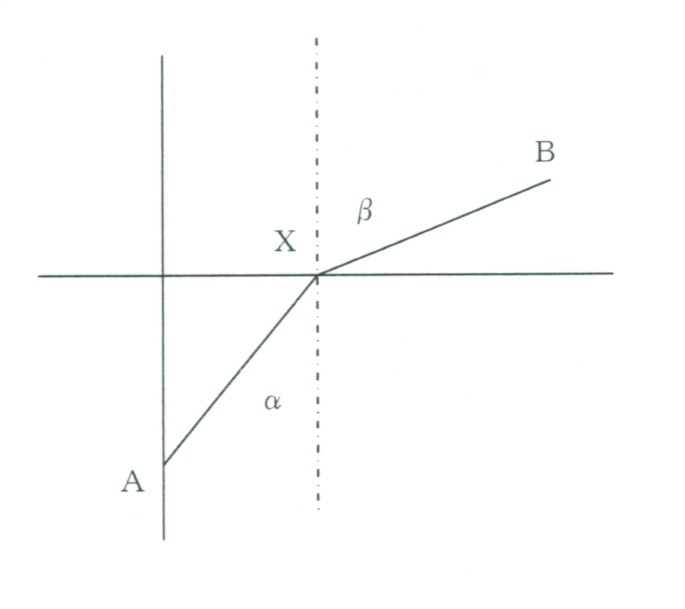 水面をx軸とし、座標(0,-a)にある点光源Aから出た光が、水面上の点X:(x,0)を通り、定点B:座標(b,c)に達したとすると、それに要する時間Tはxの関数となる。水中の光速度をu、空気中の光速度をvとすれば、
水面をx軸とし、座標(0,-a)にある点光源Aから出た光が、水面上の点X:(x,0)を通り、定点B:座標(b,c)に達したとすると、それに要する時間Tはxの関数となる。水中の光速度をu、空気中の光速度をvとすれば、
T(x)=(a2+x2)1/2/u+(c2+(b-x)2)1/2/v
所要時間が最小になるためには、T(x)をxで微分し、それが0であれば良い。よつて、
x/(a2+x2)1/2u=(b-x)/(c2+(b-x)2)1/2v
これは、図のように、水中での光の入射角をα、屈折光が空気中に出たときの屈折角をβとすれば、スネルの法則:sinα/u=sinβ/vと同じである。
人命救助とスネルの法則
 幾何光学
幾何光学
コメント