複素解析と正多角形の幾何学

左図のように、一般に、単位円に内接する正n角形P₀P₁P₂・・・P_k・・・P_n-2P_n-1において、直線P₀P_kの長さをρ_k(k=1,2,・・・n-1)としたとき、それらn-1本の線分の長さの積、ρ₁ρ₂・・・ρ_k・・・ρ_n-2ρ_n-1をA_nとすれば、
A_n=n　　　　　（1）
が成り立つ。まず簡単な場合から、（1）式を順次証明してみよう。

n=3,4,6の場合

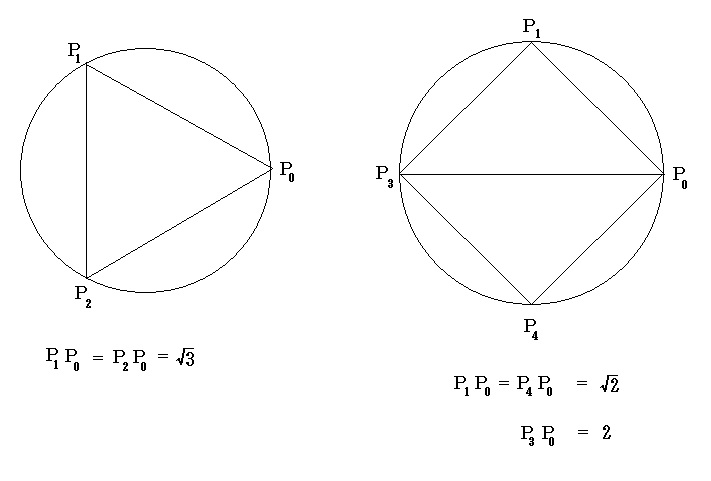
単位円に内接する正三角形の辺の長さは上の左図から√3であるから、A₃=3 になることは明らかである。また、n=4　の場合は単位円に内接する正方形の辺の長さは√2　であり、対角線の長さは2であるから。A₄＝4　も明らかであろう。

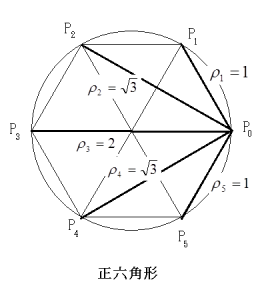
n=6 の場合も簡単に証明できる。P₀からP_kに引いた線分の長さをρ_k（k=1,2,3,4,5)とすると、その長さは図中に示した値になるので、A₆＝1××2××1＝6　となる。

n=5の場合
正五角形の場合はsin36°の値を求めなければならないので、少々難しくなるが、三角関数の訓練にもなるので、n=5の場合も証明しておこう。

ρ₁＝ρ₄＝2sin36°
ρ₂＝ρ₃＝2sin72°=4sin36°cos36°
ここで、θ＝36°、sinθ＝xとすると
A₅=ρ₁ρ₂ρ₃ρ₄ = 64x⁴ (1-x²)　　　　　、
また、5θ＝180°であるから
2θ＝180°-3θ、よつてsin2θ＝sin3θ
倍角および3倍角の公式より
2cosθ＝3－4sin²θ
2√（1-x²)=3-4x²
左辺は正であるから右辺も正。
よつてx²＜3/4 でなければならない。
4(1-x²)=(3-4x²)²
よつて、16x⁴-20x²+5＝0 　これを解くと
x²=(10±2√5)/16 となるが、x²＜3/4であるから、
x²=(10-2√5)/16 となる。よつてA₅＝5となる。

尚、正五角形の場合、ρ₂/ρ₁＝2cos36°＝(1＋2√5)/2 となるが、これは黄金比に等しい。
一般的な正n角形における証明

正n角形について、（1）式を一般的に証明するには、複素解析の手法を用いる。
3以上の整数nに対してzを未知の複素数とするn次方程式
zⁿ-1=0 　　　　　　（2）
を考える。z=1は（2）の解だから、
zⁿ-1=(z-1)f(z)　　　　　　　　　(3)
と因数分解できる。ここで、
f(z)=z^n-1+z^n-2+…+z²+z+1　　　　　（4）
であり、ｆ(1)=nである。
一方、方程式（2）はn個の解を持ち、それは、1,e^i2π/n,e^i4π/n,…,e^i2πk/n,…,e^i2π(n-1)/nとなるが、これらは複素平面の原点を中心とする単位円の円周上にあり、単位円に内接する正n角形の頂点、P₀,P₁,…,P_k,…,P_n-1に対応している。よつて、因数定理を複素数まで拡張すれば、（2）式の左辺zⁿ-1は、次のように因数分解できななければならない。
zⁿ-1=(z-1)(z-e^i2π/n)(z-e^i4π/n)…(z-e^i2πk/n)…(z-e^i2π(n-1)/n)　　　　（5）
（3）と（5）を比較すると、f(z)は次の式も満たさなければならない。
f(z)=(z-e^i2π/n)(z-e^i4π/n)…(z-e^i2πk/n)…(z-e^i2π(n-1)/n)　　　　　　　　　　　　　(6)
(6)式はzの恒等式だから、これにz=1とおくと、
(1-e^i2π/n)(1-e^i4π/n)…(1-e^i2πk/n)…(1-e^i2π(n-1)/n)=f(1)=n　となり、両辺の絶対値をとると、
｜1-e^i2π/n｜・｜1-e^i4π/n)｜・…・｜1-e^i2πk/n｜・…・｜1-e^i2π(n-1)/n｜=nとなり、絶対値｜1-e^i2πk/n｜はP₀とP_kとの距離ρ_kに等しくなるので、
A_n=ρ₁ρ₂…ρ_k…ρ_n-1=n
となる。
尚、この問題はＴ大学の理学系分野の大学院入試の過去問から引用した。