水中の物体は物体が押しのけた水の重さだけ軽くなる
中学校で習うアルキメデスの浮力の原理には、物体が押しのけた水の量が関係するので、アルキメデスが、いろんな形状の立体の体積を知っていたことは容易に想像できるが、球の表面積が、大円の面積の4倍になることも知っていたという。微積分学を知っていれば、体積も表面積も簡単に求めることができるが、紀元前3世紀に、どのようにして球の表面積に辿り着いたのだろうか。NHKの人気番組「チコちゃんに叱られる」にあやかり、「たぶん、こうだったんだろう劇場」を考えてみた。
球を考えるまえに、まず、円について考えると、半径rの円の円周の長さは2πrである。これは、円周率π(パイ)の定義でもあるが、円周の長さは、円に内接する正n角形の辺の長さの和より長く、外接する正n角形の辺の長さの和より短いことから、アルキメデスは角数nを増やしながら円周率の値を3桁の精度で3.14と求めたという。
一方、円の面積は図1のように円に内接する正n角形を二等辺三角形に切り分けると、三角形の面積は底辺の長さと高さの積の半分であるから、正n角形の面積は、横と縦の長さが、それぞれ、円周と半径からなる長方形の面積2πr2の半分に収束することから求めることができる。
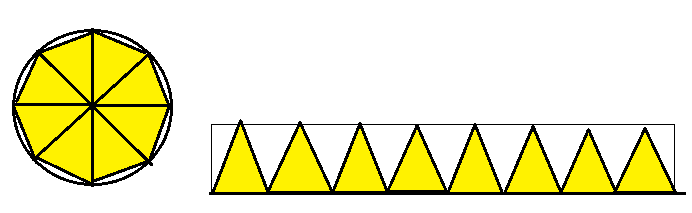
円の場合との類推から、球の場合も、球をまず多面体で近似し、多面体の面を底面、球の中心を頂点とする錐の体積が、底面の面積と球の半径の積の1/3になることから、球の表面積Sと球の体積Vの間には、V=S r/3なる関係があることを知ったに違いない。ここで錐の体積が底面積と高さの積の1/3になることは図2のような具体例から理解できる。
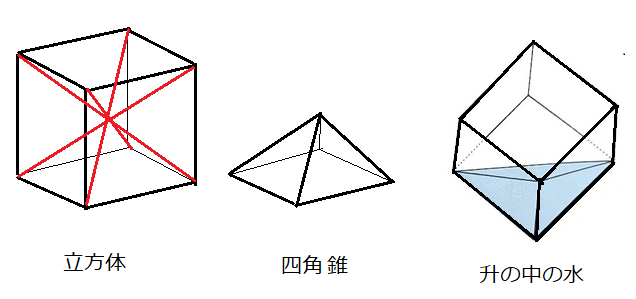
立方体は6個の四角錐からなるので、その一つの四角錐の体積は、立方体の体積の1/6であり、右図の升のなかの水は三角錐になるが、その体積も升の容積の1/6である。底辺の形によらず、錐の体積は底面の面積と高さの積の1/3である。
球の表面積をSと体積Vの関係が分かったので、一方が分かれば他方も分かる。Sを測るのは困難だが、球を水に沈めて体積Vを測れば、表面積Sは、S=3V/rと求まる。

いやいや、上の推論は、今なら何も問題ないが、当時は技術的な問題があるんだよ。アルキメデスは、それも克服して、球の表面積を求めているが、チコちゃん、それ、なんだか分かるかい?
図2のようにして角錐の体積は簡単に分かるが、球を水に沈めてその体積を測るには、正確な球を制作しなければならない。しかし、真球をつくる技術は近代になってからであり、アルキメデスの時代には、まだ大まかな球しか作れなかったと思われる。アルキメデスは、実際には、体積よりも先に、球の表面積を直感的な思考によって求めたようである。
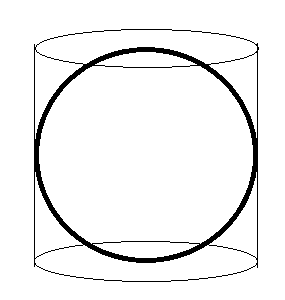
体積を知らなくても、直接、球の表面積を求める、驚くべき、しかし、簡単な方法がある。図3のように球に外接する円柱を考え、球の表面を円柱の側面に投影すると球の表面積は円柱の側面積に等しくなる。アルキメデスは、自ら発見したその方法が大変気に入り、自分の墓に図3と同じ図を書き入れるように遺言したと伝えられている。アルキメデスは、浮力の原理よりも、球の表面積の公式のほうを墓場まで持って行きたかったようである。球の表面積と円筒の側面積はなぜ等しいかについては、このHPの「球の表面積の直感的な求め方」を、ぜひ参照されたい。
たぶん、こうだったんだろう劇場 ー完ー
さてチコちゃん、表面積を測りたいもの、何かある? なに?チコちゃんのその頭の表面積? いや、さすがにそれはアルキメデスにも無理だと思うよ。


コメント