斜面を転がり落ちる円柱

　図1のように、傾斜角θの斜面を、質量M、半径α、中心軸の周りの慣性モーメントIの円柱が滑らずに転がるとき、斜面に垂直方向では、重力の成分と抗力の成分とが釣り合うので、当然、斜面に垂直方向の運動は存在しない。

　しかし、円柱の運動には、斜面に沿っての運動と中心軸のまわりの回転運動とが存在する。斜面に沿って下方方向を、座標xの正方向に選ぶと、円柱は、重力のx成分と抗力のx成分Fとによって、斜面を転がり落ちる。そのころがり運動は、xの正方向への並進運動と重心のまわりの回転運動とが連動した複合運動である。

　ころがり運動を分解した二つの運動は、Fによって連動しているので、Fは並進と回転の二つの運動の両方に現れ、その運動方程式は、次のような連立運動方程式で表される。

　（1-1）は円柱のｘ方向への並進運動に対する運動方程式であり、(1-2）は重心の周りの回転の運動方程式である。円柱は滑らずに転がるとすれば、v=αωでなければならないので、連立方程式の未知数はVとωのどちらかとFの二つである。Ｉ＝Mα²/2として、連立方程式の解くと、加速度、角加速度、抗力Fは次のように表される。

　これで、運動学としては完全に解けたことになるが、これだけでは抗力Fが、円柱のころがり運動に、どのような動力学的な役割をしているかが分からない。運動方程式から先に、Fを消去すると、Fが消えた式から、加速度も角加速度も決まり、Fは運動に無関係のように思えるからである。

　しかし、ここで、一歩、踏み込んで、運動方程式を動力学的に解くと、Fの役割が明確になる。(1-1)の両辺に速度ｖを掛け時間で積分し、一方、(1-2)式の両辺には角速度ωをかけ、時間で積分すると、次の連立方程式が得られる。

　ここで、dxはvdtであり、円柱の重心の変位であり、力の作用点の変位ではないことを強調しておこう。(2-1)は並進運動のエネルギーがMv²/2と表すことができることを示すとともに、左辺は並進運動になされた仕事であり、それが並進運動の運動エネルギーの増分に等しいことを示している。(2-2)は回転運動に対しても同様なことが成り立つことを示している。さらに、抗力Fのする仕事Fdxは、並進運動には負の仕事として寄与し、回転運動に正の仕事として寄与していることも示している。両式を加えれば、抗力Fのする仕事は消え、ころがり運動に対するエネルギー保存則が次のように導かれる。

　連立運動方程式から、動力学的に仕事とエネルギーの連立方程式を導き、さらに、エネルギーの保存則(3)式を導く過程には重力の仕事によって得られた力学的エネルギーが運動にどのように配分されるかが分かる。抗力Fは斜面と円柱の間での静止摩擦力であり、その作用点が動かないが、Fが仕事をしても不都合なことは何も起こらない。

　しかし、40年まえにアメリカでは発表された論文Pseudowork and real work(Bruce Sherwood：Am.J.Phys.Vol.51-7,(1983) p.597-602)は、最初から、(2-1)と(3)を持ち出して比較し、（３）式の左辺がreal workであり、（2-1）式の左辺は抗力Fを含むので真の仕事ではなく、擬の仕事Pseudoworkだという。それなら同じ理由で(2-2)式も真の仕事ではなくなる。

　真の仕事でない二つの仕事を加え合わせた（3）式は真の仕事になるという矛盾に陥っている。（2-1）も（2-2）も、さらに両者を加えた（３）式も運動方程式から導かれた真の仕事である。本来、一対の仕事として考えるべき、(2-1)と(2-2)とを無理に引きはがし、その片方だけを（3）と繋ぎ合わせた結果、Pseudoworkなる仕事のようで仕事でない不可解な仕事を考えざるを得なくなっている。

　ニュートン力学の完成から300年以上が経過した現在において、力学に仕事の化け物や仕事の幽霊などが入り込む余地はない。

　「エンジンがなくても抗力のする仕事で車は走る」との主張はトンデモ説であるが、「エンジンがあれば、抗力がなくても車は走る」との主張も同じくトンデモ説である。正しくはエンジンの仕事と抗力の仕事で車は走る。エンジンと車の共同作業で車が走るのに、一方だけを仕事として認め、目立たない抗力のする仕事を継子扱いし、仕事と認知しないのは不条理である。

　さて、物理の先生に考えてほしい問題はこれからである。次の図２のように加速中の車だが、前輪駆動の車の前輪のタイヤには水平抗力Fが進行方向に働き、後輪のタイヤにはｆが後ろ向きに働く。抗力Ｆとｆは車の運動にどのような役目をしているだろうか。

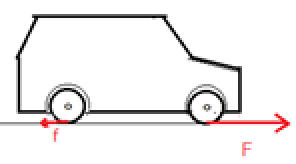
　エンジンが車の前輪の回転に仕事をして前輪が回転するのは小学生にも理解できるが、抗力Fも駆動輪の回転に、逆回りのトルクとして働き、負の仕事をし、同時に並進運動に正の仕事をしていると考えるべきではないだろうか。さらに後輪に働くｆは、車の並進運動に負の仕事をして、後輪の回転に正の仕事をすると考えれば、エンジンが生み出したエネルギーが滞りなく車の並進運動や後輪の回転運動に伝わる。

　車がエンジンブレーキで減速する場合は、図２の抗力Fもｆも向きが反転し、エネルギーの移動も逆向きになり、並進運動のエネルギーはエンジンの内部に戻され、そこで摩擦熱として消費される。車がエンジン車でなく、電気自動車では、減速するっとき、並進運動のエネルギーは、摩擦熱として無駄に捨てられることなく、バッテリーの静電エネルギーとして回収される。

　エネルギーを生み出す仕事だけが仕事ではない。エネルギーを生み出すことはできなくても、車の抗力やブランコの張力のように、運動から運動へエネルギー伝える仕事は目立たないが、日常の力学現象では極めて重要な仕事である。抗力は作用点が動かないことを理由に、その仕事を仕事と認めず、継子扱いする時代は、ニュートンの運動法則が確立された、とうの昔の時点で終わっている。抗力のする仕事を否定するのは運動法則を否定するに等しい。

　運動法則は力の作用点が動くか動かないかで、力を一切区別していない。また、昔も今も高校物理教科書には、力学での仕事は、力と、力を受けた物体の変位との内積と定義されている。教科書の作成には多くの物理関係者により、改定に改訂を重ねて長い年月をかけて完成されている。教科書の仕事の定義を変更してでも、抗力の仕事を否定したいなら、それなりの明確な根拠を示すべきである。

　教科書の仕事の定義は初心者向けの定義だとか、物体と書かれているが、質点に限定された定義だとか、支離滅裂な理屈は通らない。定理は法則ではないが法則に基づいた定義でなければ、定義の意味はない。抗力のする仕事に対する時代錯誤の偏見を改め、抗力の仕事を正当な仕事として認知すべきである。

　入試の力学の多くは単一運動であるが、日常の運動では複数の運動が連動した複合運動が圧倒的に多い。入試重視の裏で、抗力の仕事が運動と運動との間でのエネルギーの伝達に果たしているの役割が軽視されている。物理の先生には一度、複合問題を解いて頂きたい。