今度は草原にウサギとともに、ウサギを捕食するキツネが生息しているとしましょう。ウサギの個体数をX1、キツネの個体数をX2として、X1とX2とが時間的にどのような変化をするかを考えてみましょう。
複雑系の数理1で、生存競争がある場合のウサギの増殖率をa-bXと表わしましたが、今度はウサギを捕食するキツネも生息しています。キツネの個体数X2が増えると、ウサギはキツネに食べられてウサギの増殖率が減ります。この効果を取り入れるには、ウサギの増殖率に-cX2をつけ加えればよいでしょう。つまり、
(dX1/dt)/X1= a1-b1X1-c1X2 (1)
となります。a1、b1、c1はいずれも正の定数とします
一方、キツネの増殖率は-a2-b2X2+c2X1と表わされるでしょう。ウサギがいなければ、キツネは餌がありませんので、その場合の増殖率、-a2-b2X2は負になり、キツネは絶滅することになります。しかし、ウサギがいれば、キツネの増殖率が正になることができます。a2、b2、c2をいずれも正の定数として、キツネに対する微分方程式は次のように表わされます。
(dX2/dt)/X2= -a2-b2X2+c2X1 (2)
右辺第二項、-b2X2はキツネの生存競争による増殖率の減少を表わしています。(1)と(2)からなる連立微分方程式を解けばウサギ、およびキツネの個体数の時間的な変化が分かりますが、これを解析的に解くことはできません。敢えて解きたいなら数値計算するほかありません。 しかし、解の大体のふるまいなら具体的に解かなくても分かります。6個の正の数のパラメーターa1、b1、c1、a2、b2、c2、の値によっては、ウサギとキツネの個体数のそれぞれが、一定値に近づく場合、キツネが絶滅し、ウサギの個体数が一定値に落ちつく場合などが考えられます。
まず、b1=b2=0の場合を考えてみましょう。つまり、ウサギもキツネも、それぞれ種の中での生存競争はないとし、連立微分方程式を
(dX1/dt)/X1= a1-c1X2 (3)
(dX2/dt)/X2= -a2+c2X1 (4)
としてみましょう。
ウサギの増殖率はキツネの個体数に依存し、a1-c1X2ですから、ウサギは、X2 < a1/c1のとき増加し、X1 > a1/c1 のとき減少します。一方、キツネの増殖率はウサギの個体数に依存し、キツネは、X1 > a2/c2のとき増加し、X1 < a2/c2のとき減少します。つまり、X1X2平面を次の4つの領域に分けて考えることができます。
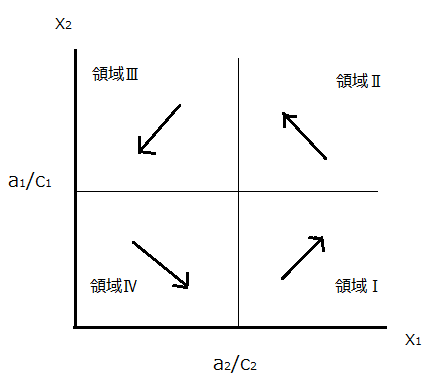
領域Ⅰ:X1 > a2/c2, X2 < a1/c1 では、X1とX2はともに増加
領域Ⅱ:X1 > a2/c2, X2 > a1/c1 では、X1は減少、X2は増加
領域Ⅲ:X1 < a2/c2, X2 > a1/c1 では、X1、X2はともに減少
領域Ⅳ:X1 < a1/c1, X1 < a1/c1 では、X1は増加、X2は減少
以上のことからウサギもキツネもその個体数が周期的に変動することが分かります。草原にウサギが増えると、キツネの餌が増えることになるので、キツネも増え始めます(領域Ⅰ)。しかし、キツネが増えすぎると、ウサギは食べられ、うさぎが減少し始めます(領域Ⅱ)。しかしウサギが減少すると、餌が足りなくなるので、キツネも減少します(領域Ⅲ)。キツネが減るとウサギはあまり食べられることがないのでウサギが増えはじめます(領域Ⅳ)。Ⅰ~Ⅳの過程を繰り返し、ウサギとキツネの個体数は同じ周期で増減しますが、キツネの変動は、ウサギの変動に1/4周期分だけ遅れることになります。
(3)と(4)式、より一般的には、(1)と(2)で表される連立方程式をロトカ・ボルテラ方程式といいます。これはアドリア海の漁獲量の変動からボルテラが考えついた連立微分方程式です。草原のウサギとキツネ、湾内のサバとフカのように食われる者と食う者が共存しているとき、ロトカ・ボルテラ方程式に従って、両者の個体数が周期的に変動することになります。
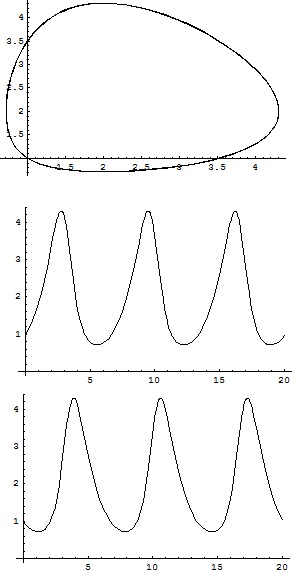
左図は数式ソフトMATHEMATICAを用いての、ロトカ・ボルテラ方程式の計算例です。一番上の図で、横軸X1は被捕食者(ウサギ)、縦軸X2は捕食者(キツネ)の数をあらわしています。時間とともにウサギとキツネの数を表す代表点(X1,X2)が閉曲線の上を反時計まわりに動いていくことになります。その結果、ウサギの数は真ん中の図のように、そしてキツネの数は一番下の図のように、どちらも周期的に増減します。この計算では(3)および(4)式において、a1=1,c1=0.5,a2=1,c2=0.5としました。
この場合、なぜ、点(X1,X2)は閉曲線上を動くのか、数学的な説明をしておきましょう。(3)式および(4)式の両辺にそれぞれ(a2-c2X1)および(a1-c1X2)をかけて加えると
(a2/X1 -c2)dX1/dt+(a1/X2 -c1)dX2/dt=0 (5)
これから
d/dt(a2logX1-c2X1+a1logX2-c1X2)=0 (6)
さらに a2logX1-c2X1+a1logX2-c1X2=一定 (7)
となり、(7)式で表される閉曲線に沿って(X1,X2)が変化することになります。
化学反応において、X1,X2 を異なるイオン濃度とすると、イオン濃度の変化はそれ自身の濃度のみならず、他のイオンの濃度にも依存することになります。二つのイオンがウサギとキツネのような関係にあると、イオン濃度が周期的に変化し、それが色の周期的変化として現れる場合があります。これはベレーソフ・ジャボチンスキー反応と呼ばれています。
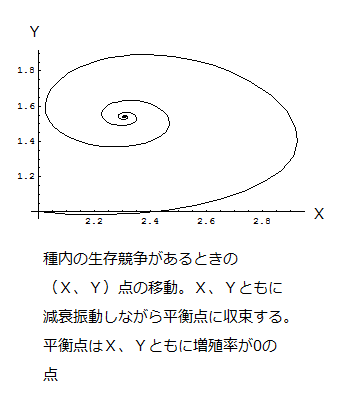
(7)式のように種内の生存競争がない場合には両種の個体数が閉曲線に沿って変化するため、両種とも、個体数が周期的に変動しますが、生存競争がある場合は、閉曲線は存在しません。下の図は生存競争がある場合ですが、係数を適当に選ぶと、このように平衡点に収束することがあります。この例では二種の個体数はともに減衰振動しながら、平衡点に近づき、一定数となり、二種が共存できることになります。(なお、図ではX1 → X, X2 → Yと変えて描いています。)
自然界にはいくつかの種が、捕食関係のみならず、天敵、共生などの関係を保ちながら共存しています。例えば、アリとアブラムシとテントウムシなら、アリとアブラムシは共生の関係にあり、テントウムシとアブラムシは捕食と被捕食、アリとテントウムシは天敵の関係ですが、三種の場合のそれぞれの増殖率も三種の間の関係を取り入れた三元連立微分方程式で表されることになります。
複雑系の数理2
 数理生態学
数理生態学
コメント