複雑系の数理1

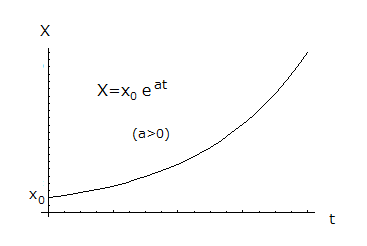
　広い草原にウサギが生息しているとしましょう。食糧となる充分な草があり、天敵もいないとすると、ウサギにとってこの草原は平和な楽園であり、ウサギの個体数Xは時間tとともに指数関数的に増えると考えられます。つまり、aとx₀を定数として
　　　X= x₀ e ^at　 (1)
と表わされるでしょう。（1）式は元金x₀を年利率aの複利で預金した場合の預金高の変化と全く同じ式です。aが正ならば、指数関数的に増加し、aが0ならば、タンス貯金とで同じでXはいつまで経っても最初の値x₀から変化しません。もし、aが負の場合は時間とともに指数関数的に減少します。

（1）式を時間tで微分すると、
　　dX/dt=a x₀e^at＝aXとなり、これから
　　　(dX/dt)/X ＝a 　　　　 (2)
となります。つまりウサギの個体数の変化が（1）式で表わされるとき、Xは（2）のような微分方程式を満たすことになり、今度の場合は、aはウサギの増殖率になります。
ウサギの個体数Xが（1）式に従って指数関数的に増えると、いくら広い草原にも、やがて、餌が足りなくなり、生存競争が起き、ウサギの個体数はどこまでも指数関数的に増えることはできなくなります。この場合、ウサギの増殖率は一定でなくなり、ウサギの個体数Xに依存して減少すると考え、増殖率をaのかわりにa－bXと置き換えればよいでしょう。そうすれば、微分方程式は（2）のかわりに、
　　　(dX/dt)/X ＝a－bX　　　（3）
となります。微分方程式（3）は非線形の微分方程式になりますが、変数分離形ですので、大学1年程度の数学を理解していれば解析的に解けます。しかし、微分方程式を具体的に解かなくても解の振る舞いの大体の様子は次のようにして分かります。
　bXがa に比べて無視できるぐらい、Xが小さいときには、Xは（1）と同じく、指数関数的に増大するでしょう。しかし、Xが増えbXがaに限りなく近づくと、増殖率a－bXも限りなく0に近づくので、Xの値は一定値a/bを超えることができなくなり、下の図のように、ウサギの個体数は一定値a/bで飽和することになります。
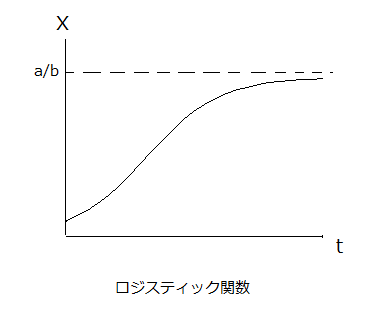　方程式（3）をロジスティック方程式、その解である左図のような関数ををロジステイック関数と呼びますが、天敵のいない平和な草原も、ウサギが増えすぎると食料不足に陥り、ウサギは一定数以上増えることはできないことを示しています。次に、この草原にウサギにとって恐ろしいキツネも生息している場合はどうなるでしょうか。ウサギはキツネに食べられてしまい、草原のウサギは絶滅するでしょうか？その場合のウサギとキツネの運命については次回にお話しすることにしましょう。