1.はじめに
「足で地面をうしろに押すと、足は反作用として地面から前向きの力を受けるから、人は歩けるのだよ」と小学生のとき習ってから70年が過ぎた。テレビでは宇宙船のなかを、人が壁からの抗力を利用して移動する様子が放映され、地上では田舎のオンボロバスが走っていたデコボコ道は、今では舗装され電気自動車が走っている。
そんな時代に、遥か昔のニュートン以前にタイムスリップしたかのように、道路から受ける抗力やブランコの張力などの作用点の動かない力は、一切仕事をしないとする短絡的な思考から生まれたPseudowork説1)が、30年間に亘り物理教育界を席巻していると知らされたときは青天の霹靂であった。足で地面を押しても地面は動かないが、その反作用を受けて人は、その方向に動いているのに!進行方向に働く外力は、足が道路から受ける抗力以外に存在しないのに!
力学の根幹に関わることについては、直感だけではなく、運動法則に基づき、地に足のついた議論をすべきだが、抗力が仕事をすると言えば、作用点動かない抗力が仕事をする筈はないとの反論を四方八方から受ける。しかし、運動法則は力の作用点が動くか動かないかで力を区別していない。抗力が仕事をすると考えてはならないとする力学的根拠は運動法則のどこにも存在しない。抗力が仕事をすれば不都合なことがあるのだろうか。
2.抗力のする隠れた役割
車が道路を走るには、エンジンのする仕事と、駆動輪が道路から受ける抗力のする仕事の両方が必要である。エンジンが仕事をすれば駆動輪が回転するが、そのエネルギーが並進運動に伝わるためには、駆動輪が道路から受ける抗力のする仕事が必要である。抗力は、駆動輪の回転に対しては文字通り抗い、負の仕事をするが、同時にその分、並進運動に正の仕事をするので、抗力が仕事をしても、エネルギー保存則に反しない。
エネルギーを生み出すことができない抗力は、並進運動に仕事をするために必要なエネルギーを駆動輪に負の仕事をすることによって得ている。道路から抗力を受けなければ、側溝に落ち脱輪した車のように、いくらアクセルを踏んでも駆動輪が空転するだけで、そのエネルギーが並進運動に伝わらず車は走れない。
抗力がエネルギーを生み出すことはないが、抗力の仕事なしでは、複合運動での運動間のエネルギーの伝達を説明できない。直感は大切ではあるが、運動法則を無視して直感だけに頼り、抗力の仕事を否定すれば、ニュートン力学から痛烈な反撃を受けることになる。仕事にはエネルギーを生み出す仕事だけでなく、運動から別の運動へエネルギーを伝える仕事もなければならない。
抗力のする仕事を否定するのは、地動説を否定して現代に天動説を復活させるに等しい愚行である。エネルギー伝達に果たす抗力のする仕事を正しく議論せず、安易に力学的根拠のない幻の仕事で置き換えるのは、見えない箇所を手抜きした違法建築のようなものであり、どこかに綻びが生じ自壊しよう。
3.静力学と静止摩擦力
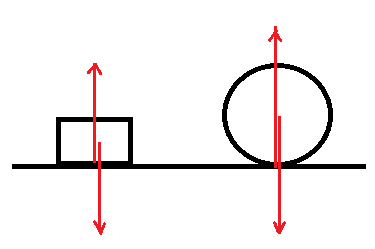
静力学によれば、物体が静止状態を維持するには、物体に働く力の合力が0であるとともに力のモーメントもゼロでなければならない。
図1のように水平な机の上に置かれた直方体と円柱には、重力と机から受ける垂直抗力とが働くが、どちらも上記のつり合いの条件を満たしているので、直方体も円柱も静止することができる。図1の状態から、図2のように机を水平から一定の限度内で傾けると、斜面から受ける垂直抗力の向きが変わり、重力と垂直抗力とがつり合わなくなるが、傾いたことで直方体も円柱も斜面から新たに静止摩擦力Fを受ける。しかし、その結果は直方体と円柱では異なる。
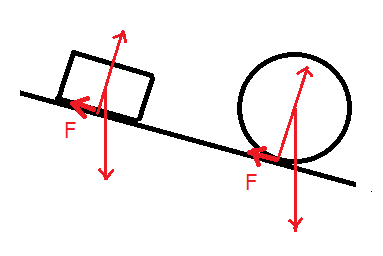
直方体では、机を傾けても、つり合いの条件を満たし、静止したままだが、円柱ではつり合いの条件が破れ動き出す。静止摩擦力は、一概に運動を妨げるだけでなく、場合によっては運動を促進させることが分かる。
斜面上の円柱に、運動量や角運動量だけでなく、さらに並進や回転のエネルギーがどのようにして生じるかについては、円柱の運動方程式に基づき、重力と抗力のする仕事についての議論が必要になる。
4.円柱のころがり運動
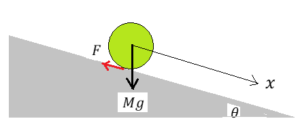
図3のように、傾斜角θの斜面を、質量M、半径a、中心軸の周りの慣性モーメントI の円柱がすべらずにころがる場合、円柱の中心の位置を示すのに、斜面に沿って下向き方向を座標xの正方向に選ぶと、円柱が受ける力のx成分は、重力のx成分と、斜面から受ける静止摩擦力Fであるが、Fの作用点は動かない。しかし、Fは、円柱の並進運動と重心のまわりの回転運動の両方に作用する。並進と回転の二つの運動は、F によって連動し、円柱の運動方程式は、次のような連立方程式になる。
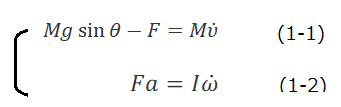
ここで、 vおよび ωは、それぞれ、重心の速度 および回転の角速度 であり、それぞれの時間微分を変数の上に・を付すことで、加速度と角加速度を表すとする。円柱がすべらずにころがるには、 aω=vが成り立つので、連立方程式の未知数は、v とω のどちらかとFの二つだが、初期条件を与えれば、vもωもFも決まり、運動量も角運動量も決まる。
円柱の運動を知るだけなら、仕事を考える必要はないが、並進運動も回転運動も、運動には、運動量や角運動量だけでなく、それぞれにエネルギーが伴う。一般に複数の運動が連動した複合運動では、初期条件として与えられたエネルギーや、動力源のエネルギーが、各運動にどのようなしくみで、どう配分されるかを知る必要がある。それには、運動方程式から、さらに仕事とエネルギーの関係式を導く必要がある。
(1-1)の両辺に速度v をかけ時間tで積分し、一方(1-2)式では両辺に角速度ωをかけ、同じく時間tで積分すると、仕事とエネルギーに関する連立方程式が導かれる。
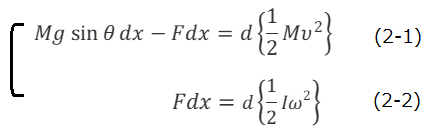
ここで、Fの作用点は動かないが、dxは vdtであり、時間間隔dt での円柱の重心の変位であり、Fの作用点の変位ではない。仕事を表す(2-1)と(2-2)の左辺は、どちらも力と物体の変位との内積である。式(2-1)と(2-2)は、並進および回転の運動のエネルギーが、それぞれの右辺の{}の中のように表されることを示し、 各運動になされた左辺の仕事が、その運動のエネルギーの増加に等しいことも示している。
(2-1)式と(2-2)の連立方程式から、抗力Fは,並進運動に対しては負の仕事をし、同時に回転運動に対しては、同じだけの正の仕事をすることを示している。抗力のする仕事を否定しては、(2-1)式だけでなく、(2-2)式も否定され、回転運動がエネルギーを得ることを説明できない。(2-1)式と(2-2)式を加えれば、抗力Fのする仕事は消え、ころがり運動に対する仕事とエネルギーの関係式は次のように導かれる。
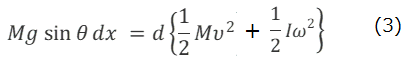
(3)式の左辺は、ころがり運動全体に対して重力がした仕事であるが、円柱の位置エネルギーの減少分でもある。右辺は円柱の運動エネルギーの増加分だから、(3)式は円柱のころがり運動に対する仕事とエネルギーの関係式であるとともに、力学的エネルギーの保存則でもある。抗力が仕事をしてはならぬとして(2-1)や(2‐2)式を否定するならエネルギー保存則をどのようにして導けばよいだろうか。エネルギー保存則は、運動法則から導くことのできない神の領域とするなら、それはもはや科学とは呼べない。
5.Pseudowork説の誤り
30年前にアメリカで発表された前述のPseudowork説によれば、仕事は、力とその作用点の内積でなければならないとして、(3)式だけが真の仕事であり、作用点の動かない力Fを含む(2-1)式の左辺は、擬の仕事だとし、円柱のころがり運動には擬の仕事と真の仕事とが存在するとして、それを他の運動にも一般化している。しかし、この説には次のような疑問や矛盾が存在する。
- 一旦は抗力の仕事を否定しながら、それを擬の仕事と名づけただけで、抗力はなぜ仕事をすることができるようになるのだろうか。
- (2-1)と(2-2)とが一対の仕事であり、(2-1)と(3)とは対をなさない
- 本来は一対の式である(2-1)と(2-2)式とを無理に引き離しているために(2-2)式にも抗力が含まれていることを見落としている.
Pseudowork説は、創造性の欠如した学生のコピペレポートと同じく、抗力のする正と負一対の仕事を無理に引き離し、その片方だけから抗力のする仕事を判断したために、抗力の仕事が必要不可欠な仕事であることを理解できず、仕事に似て仕事でない曖昧な存在として、抗力のする仕事を「継子扱い」せざるを得ないジレンマに陥っている。
6. 車の運動
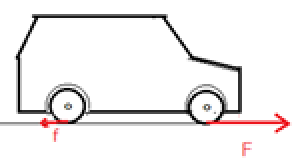
車が停止しているとき、車に働く力は重心に働く重力と4つの車輪が道路から受ける垂直抗力とが釣り合っているが、平地を加速しながら走行するとき、車には重力と垂直抗力以外に、図4のように水平抗力が加わる。前輪駆動であれば、前輪は道路から進行方向の水平抗力F を受け、後輪は後ろ向きの力fを受ける。F もf も道路から受ける静止摩擦力である。抗力F は、前輪の回転運動に対しては駆動輪の回転とは、逆回りの力のモーメントとして働き、車の並進運動に対しては、進行方向と同じ向きである。F は駆動輪の回転運動には負の仕事をし、同時に並進運動に対しては正の仕事をする。抗力 F は,その作用点は動かないので,仕事をしても、力学的エネルギーを生み出さないが、駆動輪と並進運動とに、負と正の仕事を同時にすることによって、エンジンが駆動輪に仕事をして生成されたエネルギーを車の並進運動に伝えている。一方、後輪に働くf は並進運動に負の仕事をし、同時に後輪の回転運動に正の仕事をする。fは並進運動から後輪の回転運動にエネルギーを伝えている。
電気自動車でも、加速するときは、水平抗力の向きは,図4と同じだが、減速するときは、抗力Fもfも、そ の向きは図4とは逆向きになる。電気自動車の搭載されているモーターは、加速するときは電動機、減速するときは発電機の役割をする。加速時では、モーターがバッテリーのエネルギーを使い電動機として駆動輪の回転に仕事をすると、駆動輪に前向きに働くF が駆動輪のエネルギーを並進運動に伝える。一方、減速時では、F は駆動輪に後向きに働き、並進運動から駆動輪の回転にエネルギーを伝え、駆動輪の回転が、発電機に変身したモーターに仕事してバッテリーを充電する。抗力のする仕事を正当な仕事として認知しない限り、力学教育は科学技術の急速な発展に取り残されよう。
7.仕事の定義
運動法則に、力の作用点という用語は存在しない。定義は法則ではないが、法則に準拠した定義でなければ、定義する意味はない.高校物理教科書でも、力学と熱力学での仕事は明確に区別されている。力学での仕事の定義は運動法則に基づいて定義され、熱力学での仕事は、熱力学第一法則であるエネルギー保存則に基づいた定義である。力が運動方向に働くにも関わらず、その力のする仕事を否定するなら、力学は、日常でのありふれた力学現象さえ説明できなくなる.
図3の円柱のころがり運動において、エネルギー保存則を表す(3)式を導いた(2-1)式と(2-2)式は、それぞれ、並進運動と回転運動に対して、運動法則に基づいて記述された運動方程式に、運動法則に基づく仕事の定義を正しく適用して普通に導かれる式である。作用点の動かない力のする仕事は、人知の及ばないpseudoworkなどではない。
8.おわりに
高校物理の力学は,多くが単一運動であり、入試問題も当然複合運動は出題されないので、運動間のエネルギーの受け渡しはなく、受験対策には抗力のする仕事は必要ではない。しかし、物理は受験のためだけに学ぶのではない。現実の力学現象は複合運動が圧倒的に多く、受験重視のなかで忘れられている抗力のする仕事を正当な仕事として評価すべきである。高校物理教科書の仕事の定義を変えるべきとの意見もあるが本末転倒である。
日本物理学会では、現在「物理教育における高大接続」(大学の物理教育2025 Vol.31 No.2)が進められているが、「作用点の動かない力は仕事をしない」という呪縛から解放されない限り、脱輪したまま放置されている力学教育では、高大接続などおぼつかない。高校生に抗力のする仕事を教えなくても、抗力の仕事を考える余地を残しておくべきである。抗力のする仕事をタブー視しては力学を適用できる範囲が限定されてしまう。
日常会話ならまだしも、「人はなぜ歩けるか」に対する物理教育の答が「右足出して左足出すから」だけでよいとは思えない。人の筋力やエンジンなどの動力源の仕事が、エネルギーを生み出しているのに対し、そのエネルギーを並進運動に伝えているのは、紛れもなく、抗力のする仕事である2)。
極めて不可解で、狐につままれたような話だが、これまで、関連学会は、仕事の問題は30年前にすべて解決済として、抗力の仕事に関する議論を誤概念として悉く退けてきた。さらに、抗力の仕事に関する投稿は、今後、掲載の対象外にするとのことだが、抗力のする仕事を継子扱いし、ネグレクトする力学教育に明日はこない。運動法則に基づいて正しく議論をせずに、脱輪して放置されている力学教育を、そのまま次世代に受け渡してよいだろうか。学会には、抗力が同時にする正と負の一対の仕事を正統な仕事として認知した力学教育に戻ることを強くお勧めしたい。
1)Bruce Sherwood:Am.J.Phys.Vol.51-7,(1983) p.597-602
2)後藤信行:教育の関する一言「抗力の仕事を邪魔者扱いしない力学教育を」大学の物理教育 2025 Vol.31No.3(掲載予定)


コメント