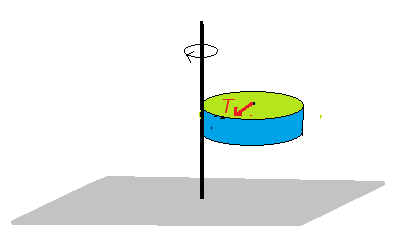
図1のように、半径r、質量Mの円柱を、力Tで引っ張って水平な台上を転がす場合について、円柱が台から受ける抗力の役割について考えてみよう。

台からの抗力Fが働かなければ、円柱は回転することはできない。抗力Fが円柱の中心軸のまわりに作る右回りの力のモーメントによって角運動量を得て、円柱は回転する。しかし、回転運動は角運動量とともに回転のエネルギーを持つ。もし、抗力Fが仕事をしないとするなら、円柱はどのようにして回転のエネルギーを得ることができるだろうか。角運動量だけでエネルギーを持たない回転運動などは存在しない。円柱の並進運動にに対しても同様である。運動量だけでエネルギーを持たない並進運動も存在しない。
運動量Pと角運動量Lが導かれれば、それから、並進および回転のエネルギーは、それぞれ、P2/2M、L2/2Iとなるから、並進や回転運動がエネルギーを持つことは、運動量と角運動量から分かるではないかという考えもあろう。しかし、それはすでに運動量とエネルギーの関係を知っているからであり、並進や回転のエネルギーも、運動量や角運動量と同じく、運動方程式から導かれるべきである。
円柱の運動は次の式(1)で示されるように並進運動と転がり運動に対する連立方程式で表すことができる。
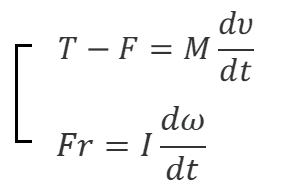
あとは滑らないという条件v=rωという条件のもとに数学を用いて式(1)を解くだけである。(1)の上式と下式を時間で積分すれば運動量にも角運動量にもFが寄与することは明らかだが、並進と回転の運動エネルギーにもFが寄与することがわかる。連立方程式(1)から次の連立方程式(2)が導かれる。
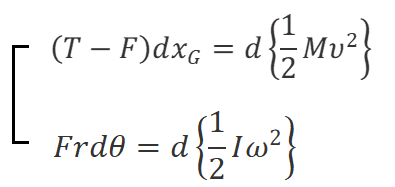
ここで、dxG=vdtであり、vは重心の速度であるから、dxGは重心の変位であり、Tの作用点の変位でもあるが、静止摩擦力であるFの作用点の変位は0である。しかし、運動法則は作用点が動くか否かで力を区別していない。連立方程式(2)は張力Tが並進運動に正の仕事をして、抗力Fは並進運動に負の仕事をし同時に回転運動に正の仕事をしていることを示している。式(2)からFを消去すると、単独な次の式が得られる。
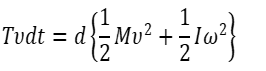
式(3)は転がり運動を一つの運動とみなしたとき、作用点の動かない抗力のする仕事は消え、左辺はTのみの仕事になることを示している。
連立の運動方程式(1)は数学を用いてどう解いてもよいから、式(1)から最初にFを消去すると、
.png)
となる。ただし、Fを消去した式(4)には、Fに関する情報がすでに失われている。式(4)からも式(3)を導くことができるが、式(4)はもはや、図1の転がり運動の運動方程式ではなく、図2のように円柱に固定軸を取り付けた回転運動の運動方程式に変わっている。
また、式(1)から抗力Fを消去した式を、次の式(5)のようにも表すこともできる。
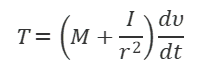
式(5)は図3のように、質量M+I/r2を持つ適当な形状の物体が力Tを受けて並進運動するときの運動方程式と同じになるが、(5)からも式(3)を導くことができる。
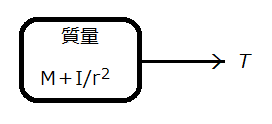
Tが仕事をすることによって得られたエネルギーがどのように使われたかは、その内訳を明確に示す連立方程式(2)を経由せずに、さきに抗力を消去した式(4)や式(5)から式(3)を導いたのでは、もとの運動が図1であるのか図2であるか、あるいは図3のように、質量も形状も異なる物体の並進運動であったかが分からなくなる。つまり、式(3)だけでは、外部の動力源が仕事をすることによって得られたエネルギーが系の並進運動と回転運動とに、どのように配分されたかが分からない。
定年後に、地域の自治会の役員(公民館長)をしたことがある。このとき、初めて会計報告を行ったが、収入と支出が一致したというだけでは、収入の全てを飲み食いに使ったのか、そうでないのかがわからない。公民館活動の正確な内容を示すには支出の内訳を明示しなければ、ドンブリ勘定の会計報告になり、公民館長は自治会総会で吊るしあげられる。
式(3)は正しい式であるが、それを導くには(2)式がなければならない。さらに式(2)を導くためには式(1)が必要である。その手順を踏まずに、いきなり(3)式を持ち出して、抗力は仕事をしないとか、式(2)の上の式はPseudoworkだとか、いずれもニュートンの運動法則を無視した「言いがかり」としか思えない。
円柱の転がり運動は数式で式(1)、さらに式(2)と表せるので、抗力のする正と負の仕事が数式で証明できるが、懸垂やスクワットで重心が持ち上がる運動を説明するのは難しい。しかし、これも人の変形運動と重心運動に分けて考えると分かりやすい。
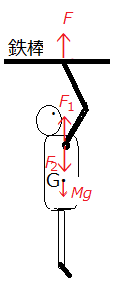
人が懸垂で重心を持ち上げるとき、人に働く外力は鉄棒から受ける抗力Fと人の重心に働く重力Mgだけである。このとき、図4のように、大きさがFと同じで互いに上下に働く二つの力F1 F2を腕の付け根に付け加えても運動には影響しない。重心を上げるには、腕の筋力に腕を間でなければならないが、FとF2とは、腕を曲げようとする変形運動を妨げる向きに働く。つまり、FとF2とは変形運動に負の仕事をする。残りの力F1が重心運動に仕事をして重心を上に引き上げる。F1とFとは大きさは同じであるから、F>Mgであれば、重心運動に運動量と運動エネルギーを生じさせることができる。Fは変形運動に負の仕事をすることによって、その作用点が腕の付け根にいどうすると考えることもできよう。抗力Fが仕事をしても円柱の転がり運動の場合の抗力と同じく、正と負の仕事を同時にするので、エネルギー保存則に反することはない。
いくら兎年でも、地面から抗力を受けなければ、兎は飛び跳ねることはできない。亀だって地面を這うことができない。車は道路から受ける抗力がなければ、いくらアクセルを踏んでも、駆動輪が回転するだけで、そのエネルギーが車の並進運動には伝わらない。
事なかれ主義に陥り、触らぬ神に祟りなしと、波風立たないように、これまでどおりPseudowork信仰を続け、ドンブリ勘定の力学に辻褄を合わせるために、これまで多くの物理関係者によって創り上げられた高校物理教科書に書かれている仕事の定義の解釈を意図的に捻じ曲げ、そのまま放置しておくのか、それとも固定観念にとらわれず、運動法則から自然に導かれる抗力のする正負同時一対の仕事を認めるか、決断のときである。
一見、難攻不落に思えても、Pseudowork説を初めとして、運動法則を無視した力学理論は、所詮、砂上の楼閣、恐れるに足りぬ。何を躊躇するのだ、余計なことは考えず、運動法則の導くままに普通に進めばよい。大河ドラマも始まった。物理関係者のひとりひとりに問いたい、高校物理教科書の仕事の定義を無視したまま、エネルギーのドンブリ勘定を続けるつもりか、それとも抗力のする仕事を認めるか、さあ、どうする物理教育!
関連するページ:身体検査の日の思い出

コメント