いやいやしているのか、頷いているのか、天空の美女は前後左右にゆっくり首を振り、少しばかりその横顔をわれわれに見せている。支点のない天空で、月は振り子のように、地球が月に及ぼす起潮力によって前後に引っ張られながら、僅かに揺れているのである。月に秤動が生じるしくみとその周期について、直感的な説明を試みてみた。
宇宙の鉛筆
1955年、秋田県の道川海岸から日本海に向けて発射されたペンシル300は高度600mに達した。当時、日本の海岸は米軍の管理下にあり、また船舶や航空機への影響など、いろいろな制限のなかで、ロケットの発射場として道川海岸が選ばれたが、やがてロケットが大型化すると、当時の李承晩ラインを越える恐れや、さらに、その向こうの大陸へ落下する恐れが生じてきた。
その後、米軍による海岸の利用制限も緩和され、日本の宇宙基地は衛星を打ち上げるのに有利な、鹿児島県大隈半島の内之浦に移された。衛星の打ち上げ場所として、より赤道に近いところから東に向けて打ち上げれば、打ち上げ速度に地球の自転速度を加えることができるので、エネルギーの面で得だからである。とくに静止衛星は赤道上に打ち上げなければならないので、発射場は赤道近くに建設するほうがよい。現在では内之浦と、さらにその後に建設された種子島宇宙センターが衛星の打ち上げに使用されている。
鉛筆の長さ程のものから始まった日本のロケット開発は初期の固体燃料ロケットから液体燃料となり、半世紀の歳月を経た今、H2ロケットへと進化したが、打ち上げたロケットが人工衛星となり、姿勢制御をすることなく、地球の周りを長期間回ったとしたら、この巨大化した「宇宙の鉛筆」は最終的にはどのような姿勢で地球の周りをまわり続けるだろうか。
地上では、鉛筆の先端を下にして机の上に立てることはできない。鉛筆を完全に鉛直方向に向けた状態は、鉛筆に働く重力と机の面からの抗力が釣り合っているが、その状態は不安定である。鉛筆が鉛直の状態から少しでも傾くと、力の釣り合いが破れて、正味の力が現れ、それが鉛筆の傾きをさらに増幅させるからである。つまり、鉛筆の芯を下にして鉛直に立てた状態は不安定平衡状態であり、その状態にとどまることは不可能である。

安定な平衡状態と不安定な平衡状態を図1に示すような例で考えると分りやすい。左右のいずれの図でも球に働く力は釣り合っているが、右図では平衡点からどちらかに僅かでもずれると、そのずれを増幅する力が益々強くなり、不安定なその状態を長時間維持するのは不可能である。一方、左図のような安定な平衡状態では、平衡点から僅かにずれると、平衡点へ引き戻そうとする力が働き、球は平衡点の近傍で振動する。
宇宙に人工衛星として放出された鉛筆では、地球が鉛筆に及ぼす起潮力が、地球から見て、鉛筆を前後方向に引き伸ばすように働くため、軸を地球の中心に向けた状態が安定となる。宇宙の鉛筆がその状態から僅かに傾くと、起潮力はその傾きを戻す向きに働き、鉛筆の向きも、その安定状態の近傍で振動する。
重りを紐でつるした地上での振り子の振動の周期は重りの質量によらず、紐の長さと重力の加速度の大きさで決まる。また、バネに吊るされた重りでは、振動の周期は、重りの質量とバネ定数で決まる。それなら地球の周りの円軌道を周回する宇宙の鉛筆の揺れの周期はどのようになるだろうか。宇宙の振り子は地上の振り子に比べ、かなり難しい問題であるが、困難を迂回することにより、高校程度の物理の範囲で、宇宙の鉛筆の振動周期を求めてみよう。そのまえに、地球のまわりの円軌道をまわる宇宙の鉛筆に、地球が及ぼす起潮力について少々詳しく考えてみることにしよう。
地球の起潮力
地球の衛星である月は地球に起潮力を及ぼし、地球の海に潮汐を引き起こしているが、逆に、地球も衛星に起潮力を及ぼす。地球の重力場のなかで、重力の働くままに任せて運動する座標系、つまり、ケプラー運動する座標系に働く地球の起潮力を考えよう。
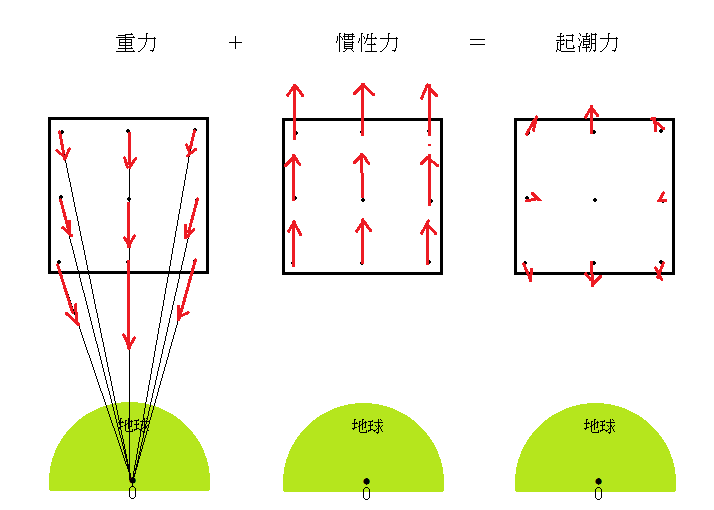
この場合、座標系の座標軸に向きは一定とする。最も簡単な場合として、地球の中心に向かって自由落下する箱をその座標系と考えるとよい(起潮力の詳しい説明については「秋の夜長の月物語(改訂版)」を参照のこと)。座標系の加速度運動による慣性力は重力を完全に打ち消すことはできない。座標系は局所慣性系であり、衛星の重心から離れると、地球の中心方向に引き伸ばす力と、水平方向に圧縮する歪み力が残る。これが、重力場の中をケプラー運動する物体に地球が及ぼす起潮力である 。ちなみに、一般相対論によれば、起潮力は曲率、つまり、時空の歪みに対応している。
人工衛星のような小さな衛星が起潮力によって破壊されることはまずないが、衛星の形状が、衛星自身の重力によってのみ、保たれている場合には、衛星が惑星にある一定距離以内に近づくと、惑星が衛星を引きちぎろうとする起潮力が衛星自身の重力を上回り、衛星は破壊される。この公転半径の限界をロッシュ限界という。1994年7月に木星に衝突したシューメーカー・レビー第九彗星は衝突寸前に二十個の破片に砕けたが、これは彗星が木星のロッシュ限界内に入り込み、木星の強い起潮力によって引きちぎられたのである。
円軌道上の衛星
地球のまわりの円軌道を運動する衛星を考えてみよう。衛星の力学的エネルギーをE、運動エネルギーをK、ポテンシャルエネルギーをUとすると、衛星の軌道が円であれば、常に
E:U:K=-1:-2:1 (1)
なる関係が成り立っている。これから、衛星が力学的エネルギーEを断熱的にε だけ失うと、衛星のポテンシャルエネルギーUは2 εだけ失われ、運動エネルギーKはε だけ増える。つまり、衛星は衛星が上空大気との摩擦などにより、エネルギーを失うと衛星の速度は増すことになる。
話は少々横道にずれるが、(1)式の関係は円軌道を運動する衛星のみならず、万有引力によって相互作用する多粒子系についても成り立つことがビリアル定理から導かれる。その場合は、E、U、およびKは、それぞれ、系全体の、力学的エネルギー、ポテンシャルエネルギー、運動エネルギーとなる。星の誕生の初期の段階において、宇宙の塵が集まると、塵同士の衝突のため、系の力学的エネルギーは熱になって失われる。系が収縮すると、ポテンシャルエネルギーは減少するが、運動エネルギーは逆に増加し、衝突はより頻繁に起こり、系は益々発熱する。つまり、系は外部に熱を放出するほど高温になり、一見、熱容量が負の状態となる。高温となり、やがて、系の内部で核融合が始まると収縮はとまり、そして系は輝く星となる。
話を人工衛星に戻し、二個の衛星を、同一平面内の、高度が異なる円軌道に、それぞれ、同じ向きにまわるように打ち上げたとしよう。上空の衛星は低空の衛星に比べ、力学的エネルギーが大きいが、運動エネルギーは小さいので、低空の衛星に追い越されながら、公転することになる。
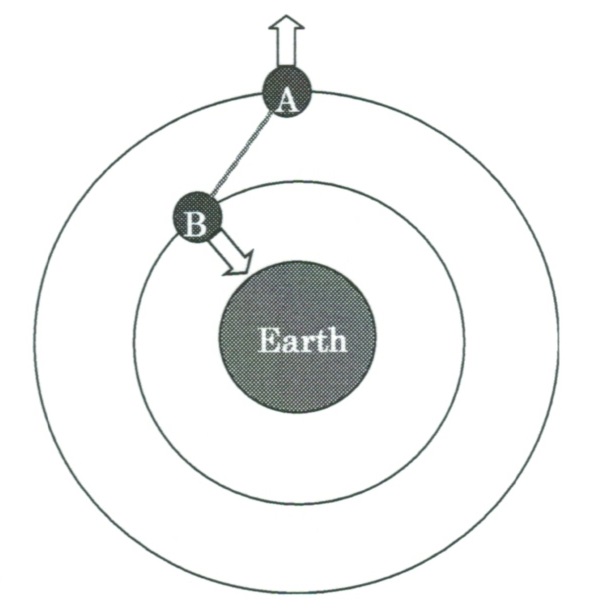
かつて、ガリレイは、紐で結ばれた重さの異なる二つの物体の落下を考え、重さによって落ちる速さが異なると仮定すると、論理的に矛盾が生じることを示し、落ちる速さは重さに無関係でなければならないとした。我々も偉大な先達の思考実験に習い、図3のように、高度の異なる二つの衛星を紐でつないで思考実験を試みてみよう。繋がれた二つの質点のうち、低空の質点Bは上空の質点Aを引っ張って運動するので、Bはますますエネルギーが小さくなって低空へと移り、上空の質点Aは前方に引っ張られエネルギーが増えるので、さらに上空へと移ろうとする。つまり、二つの質点をつないだ紐は地球の中心を向こうとする。
二つの質点を紐の代わりに軽い棒でつないだ連結衛星を打ち上げれば、衛星の軸を地球に向けて運動する状態は安定な平衡状態であり、軸を水平に向けて公転する状態は不安定な平衡状態となることがわかる。
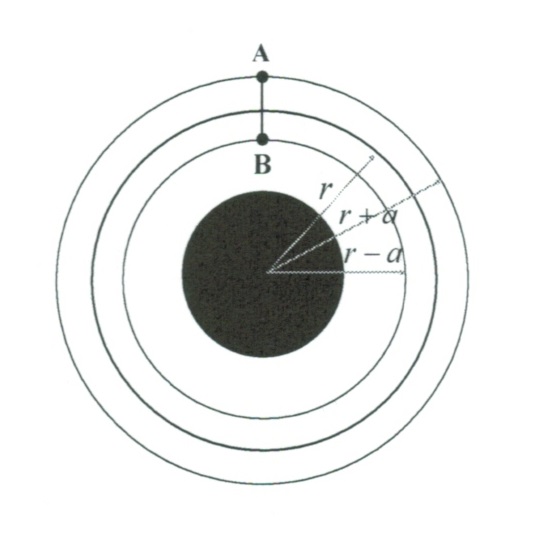
図4のように、連結衛星が長軸を地球に向けて公転するとき、二つの質点を引き離そうとする起潮力と質点を結ぶ棒の張力Sが釣り合っているが、その大きさは二つの質点に対するそれぞれの円運動の運動方程式から簡単に導くことができ、となる。ここでmは質点の質量、
は二つの質点を結ぶ棒の長さの半分、Ωは、衛星が地球の周りを公転する角速度である。
秤動の周期
連結衛星は長軸を地球に向けた状態が安定平衡であるので、この安定状態の近傍で微小振動が存在する。この微小振動が衛星の秤動である。二つの質点からなる衛星の秤動の角振動数は、図5のように、地上の重力場での振り子と比較することによって求めることが出来る。
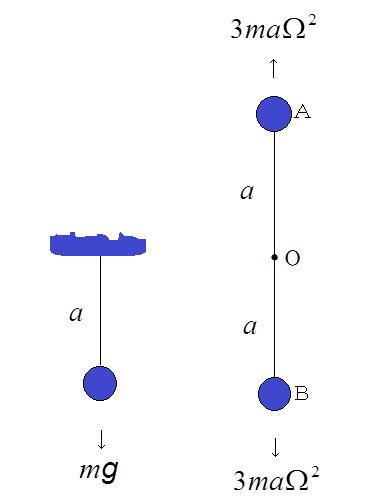
地上の振り子に働く重力のかわりに、天空の振り子では起潮力が働いている。つまり、高校物理で習う振り子の周期の式に、
置き換えればよい。また、天空の振り子の支点は連結衛星の重心となるから、振り子の長さとして衛星の半分の長さとすればよい。天空の振り子の角振動数は公転運動の角速度の
倍となることが分かる。つまり、衛星として打ち上げられた振り子は、公転軌道をを一周する間に、約1.73回振れる。
この振動数は衛星の公転運動の角速度のみに依存し、振り子の長さ、つまり衛星の長さに依存しないので、質点が直線状に並んだ衛星の秤動の角振動数もこれと同じになる。球状衛星では秤動は存在しないから、その場合の秤動の角振動数はゼロである。一般に衛星の秤動の角振動数ωは、衛星の形状によって決まり、0より大きく、軌道運動の角速度Ωの1.73 倍より小さい範囲に存在する。つまり、どのような衛星も、衛星が地球のまわりを一周する間の秤動の回数は1.73 回よりも少なくなる。

月の秤動
大昔、月がもっと速く自転していたとしても、月の内部の潮汐摩擦によって、月の自転と公転の周期はぴったりと一致すると同時に、地球による起潮力のため、月は地球の方向に少し引き伸ばされた状態で固まり、楕円体の形となったと考えられる。現在では月はその長軸を地球に向けて公転するとともに、地球に向けた軸が振り子のように僅かに振れている。この首振り運動、つまり、秤動のため、地球から月の全表面積の59%を見ることができる。しかし、地球から見た月の秤動には、みかけの秤動が加わっていて、これを差し引いたのが真の秤動になる。
みかけの秤動として、まず、考えられるのは、地球の自転に伴い、地球上の観測点の位置が、月の前面を横切ることによって生じる秤動である。月が地球の中心を見つめていたとしても、地表で観測している我々は、月の視線を横切って動くことになるので、その横顔を少し垣間見ることができる。月までの距離は38万km、地球の直径は1万3000kmであるので、このみかけの秤動の振れ角度は最大2度程度となる。
次に考えられるみかけの秤動は、月の軌道が完全な円でないため、月の自転と公転の周期は一致していても、月の自転の角速度と公転の角速度を常に一致させておくことはできない。つまり、月の公転の角速度が一定でないため、月は地球の中心をいつも見つめている訳にはいかないのである。
みかけの秤動を光学的秤動とよぶが、地球から見た秤動から光学的秤動を差し引いたのが力学的秤動とよばれる月の真の秤動である。月の力学的秤動はいろいろな周期の秤動が重ね合わさっていて複雑である。まず、月の軌道は完全な円でないので、地球からの起潮力が27.3日の周期で変動するため、その強制振動が現れると考えられる。
その他に、周期2.9年の秤動、地球の極運動 に相当する75年周期の秤動が存在すると考えられている。月は極めて球形に近いので、その秤動の周期はいずれも長いものとなっている。

コメント