連成振動の改訂版を公開しています。→改訂版
図のように、ともに質量Mの等しい二つの物体A、Bが三つのバネで水平に繋がれているとしよう。左右のバネのバネ係数をK、中央 のバネは左右のバネに比べ弱く、そのバネ係数をkとしよう。物体と床の摩擦はないものとする。
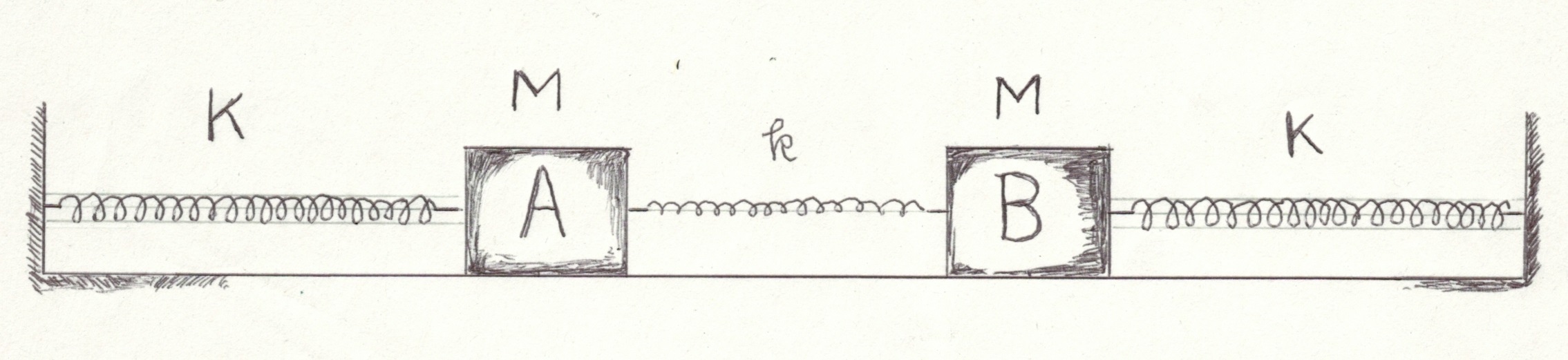
まず、中央のバネが存在しない場合を考えてみよう。そのときは、二つのバネ振動子はそれぞれ単独のバネ振動子となり、両者の角振動数(=2π×振動数)はもちろん等しく、その値はK/Mの平方根になる。次に、バネ係数がkの、弱いバネでAとBを結ぶと、この結合系は僅かに振動数の異なる二つの固有振動を持つ。固有振動の一つはAとBが同じ方向に振れる振動であるが、これを並行振動と呼び、もう一つはAとBが互いに逆方向に振れる振動で、これを対称振動と呼ぶことにしよう。
並行振動ではAとBが同位相で振動し、両者の間の距離は変わらないので、中央の弱いバネは伸び縮みせず、振動に寄与しない。よつて、その角振動数は、結合するまえの単独の振動子の角振動数と同じである。一方、対称振動ではAとBは互いに逆方向に振動するので、真ん中の弱いバネも振動に寄与する。このとき、AとBを結んだ中央のバネの中心は動かないので、対称振動では、中央のバネの中心を固定した場合の振動と同じになる。対称振動に寄与するバネはバネ定数Kのバネと、中央の弱いバネとなるが、後者は中心が固定されているので、長さが半分になっている。バネの長さが半分になると、バネ定数は2倍になる。つまり、対称振動の角振動数は(K+2k)/Mの平方根となる。
一般の振動は二つの固有振動の重ね合わせで表されるが、kがKに比べ、充分小さければ、二つの固有振動の振動数が接近しているため、振動にうなりが生じる。例えば、つりあいの位置に静止した状態から、Bのみに変位を与えて振らせると、Bの振動の振幅が次第に小さくとなるとともに、次第にAが振れだす。このとき、Aの振動の位相はBに比べ、90度遅れているため、Aが一往復する間に、Bが中央のバネを通してAにする仕事は正となる。AはBの振動からエネルギーを貰い、次第に振幅が大きくなり、逆にBはエネルギーを失い振幅が小さくなる。
その後、両者の振幅の大きさは逆転し、やがてBが止まると、Aの振動の振幅は最大となり、止まったBが再び振れだすが、今度はBの振動の位相がAに比べ、90度遅れる。つまり、Aの振動の位相は静止する前後で反転する。これをAとBの間で繰り返す。AとBの振動が中央のバネによって相互作用することによって、両者の間にエネルギーのやり取りが交互におこることになる。
以上のことを、今度は数式を用いて説明してみよう。Aの位置座標をxA、Bの位置座標をxB、平行振動の角振動数をω、対称振動のそれをω+2εとすれば、適当な初期条件を選べば、二つの固有振動が同じ割合で混じり合った振動は
xB+xA=sinωt (1)
xB-xA=sin(ω+2ε)t (2)
となる。これより、
xA=cos(ω+ε)t・sin εt (3)
xB=sin(ω+ε)t・cos εt (4)
となり、これは角振動数ω+εでの振動が、sin εtまたはcos εtの振幅変調をうけていることになる。
t=0がBを振らした瞬間であるが、このとき、Bの振幅は最大であるが、Aの振幅はゼロである。その後、Bの振幅が減少するとともにAの振幅は増大していく。この間、振動の位相は、AがBより90°遅れている。Aの振幅sin εtが最大となるとき、Bの振幅cos εtは符号が変わるので、Bの振動の位相が反転するため、今度は、Bの位相がAの位相より90°遅れ、エネルギーがAからBに補給される。
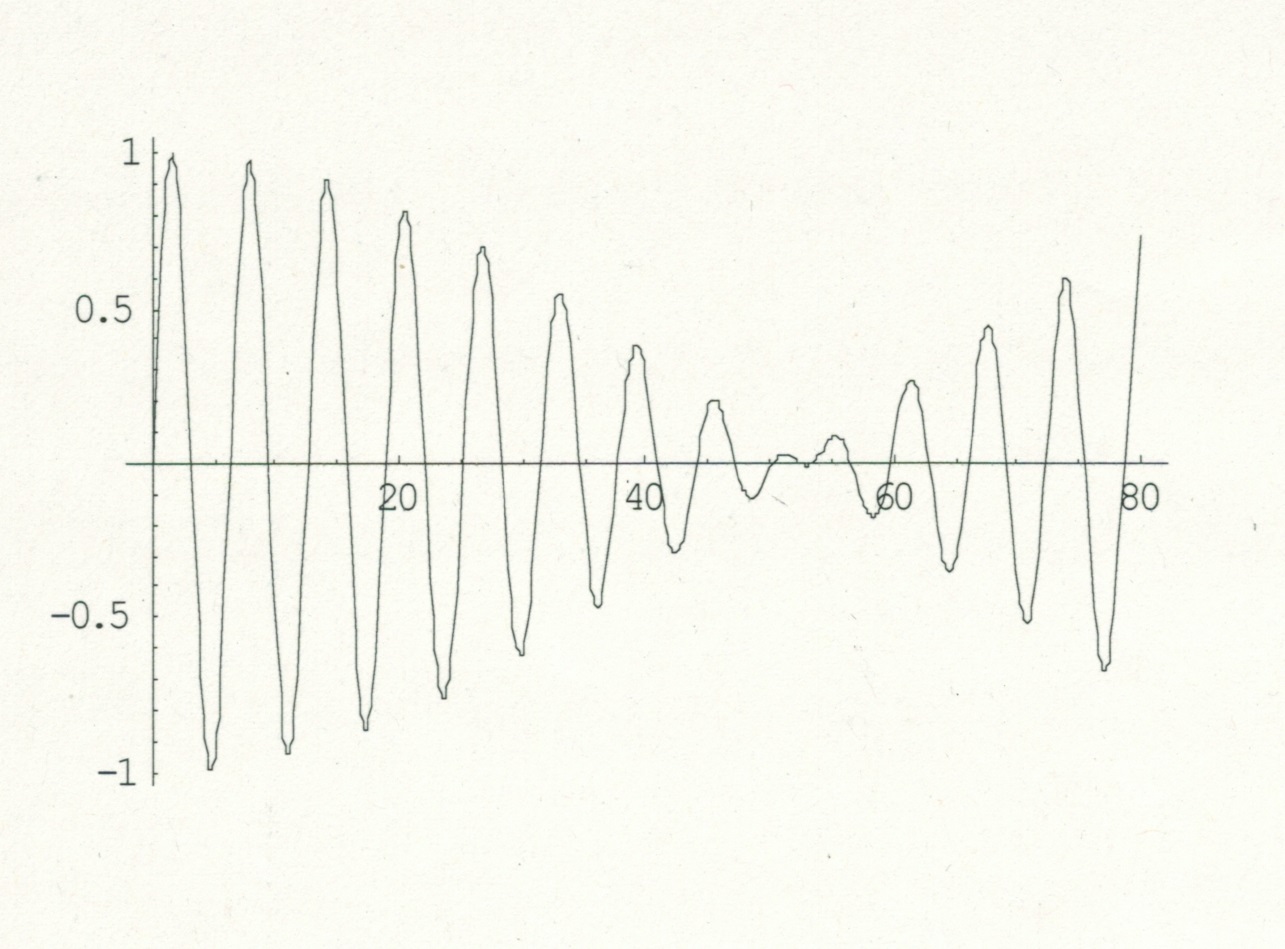
左図はω+ε=1、ε=0.03としたときの、(4)式で表されるxBの振動を、数式ソフトMATHEMATICAで計算したものである。横軸は時間であるが、振動の振幅がゼロとなる時刻で振動の位相が反転するのが見られる。
二つの固有振動のうち、平行振動は、AとBの振動の位相差はゼロであり、もう一つの固有振動の対称振動ではAとBの振動の位相差はπであり、いずれもAの振動とBの振動の間では、エネルギーの受け渡しは起こらない。固有振動の状態ではAもBも一定の振幅で振れ続ける。

コメント