ハンドゼネレーターと呼ばれる実験教材が市販されている。これを、図1のように、コンデンサーとつなぎ、そのハンドルを手で回して発電すると、コンデンサーが充電される。次に、ハンドルから手を離すと、ハンドゼネレーターは、発電機からモーターに変わり、コンデンサーに蓄えられた電気的エネルギーによってハンドルはひとりでに回転する。このとき、ハンドルは、充電するときに回した向きと同じ向きに回る。

電気自動車にも、モーターとコンデンサーが搭載されているが、モーターはモーター本来の役目と発電機の役目の両方を兼ね備えている(注:実際の電気自動車はインバータがついた交流モーターだが、ここでは簡単のため、直流モーターとしておく)。下り坂では、発電機の役目をしてコンデンサーを充電する。つまり、位置エネルギーを電気的エネルギーに変換し、それをコンデンサーに蓄えている。また、ブレーキを踏んで減速する場合も、運動エネルギーを無駄にしないで、電気的エネルギーに変換してコンデンサーに蓄える。一方、上り坂や加速するときは、モーターは本来の役目に戻り、コンデンサーの電気エネルギーを車輪の回転のエネルギーに変えている。
摩擦などによるエネルギーの損失が全くなければ、電気自動車は、外部からエネルギーを一切補給しないで、どこまでも走れることになるのだが、現実には、摩擦などによるエネルギーの損失は避けられないので、その分のエネルギーを外部電源から補給しなければならない。
電気自動車より先に、低燃費、低公害車として普及したハイブリッドカーでは、エネルギーの損失分をエンジンのエネルギー、つまり、ガソリンの化学的エネルギーで補っている。最近では、短距離の場合は電気自動車として走り、長距離の場合はハイブリッドカーとして使用するプラグイン・ハイブリッドカーも売り出されているが、電気自動車もハイブリッドカーも、モーターとコンデンサーのセットによって、エネルギーの無駄を極力抑えている点では同じである。
モーターとコンデンサーのセットは電動アシスト自転車にも取り入れられている。電動アシスト自転車はエンジンによるエネルギーの補給も、外部電源からの補給もないので、エネルギーの損失分を乗り手の筋力に頼っている。
電気自動車やハイブリッドカーや電動アシスト自転車のモーターは、好都合なことに、発電機と、電動機の役目のときとで、回転の向きが同じであるため、下り坂から上り坂へ変わっても、ギャの切り替えや配線の繋ぎ変えなどは一切必要としない。なぜ、回転の向きは同じになるのか、それを理解するために、まず、モーター(電動機)と発電機の原理について考えてみよう。
モーターの原理と発電機の原理
筆者が中学生のときの理科の授業では、(電動機としての)モーターの場合には、その回転の向きを知るのに、フレミングの左手の法則を用い、発電機の場合の起電力の向きを知るには、フレミングの右手の法則を用いなさいと教えられた。
モーターの場合には、左手を出して、親指、人差し指、中指が互いに直交するように開き、人差し指を磁界の方向、中指を回転子のコイルに流れる電流の方向に合わせれば、電流が流れている導線は親指方向の力を受け、それがモーターの回転力となる。
一方、発電機の場合には、今度は右手を出して、人差し指は同じく磁界の向きに合わせ、磁界のなかで導線を動かす方向に親指を一致させれば、その導線には中指方向に電流を流そうとする起電力が生じるというものであった。
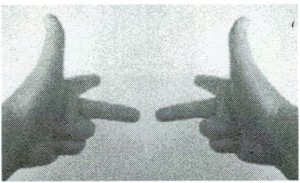
コンデンサーに繋がれたハンドゼネレーターは、発電機からモーターに変わっても、界磁として、同じ永久磁石を用いているので、磁界の向き(人差し指)は変らないが、発電機の役目の場合にはコンデンサーは充電され、モーターの役目の場合には、コンデンサーから放電されるので、電流の向き(中指)は逆になる。これから、図2のように、左右の手の人差し指を同じ方向に揃え、中指を互いに逆向きにすれば、親指は同じ方向を向く。つまり、発電機のときに回転させた向きと、モーターに変ったあとに回転する向きは同じになることがわかる。
受験参考書などには、フレミングの左手や右手の法則の覚え方として、親指、人差し指、中指の順にF(力)B(磁界)I(電流)とする方法などが紹介されているが、なぜ、モーターの場合は左手の法則で、発電機の場合は右手の法則なのだろうか。モーターも発電機も同じ法則で説明できないだろうか。それを理解するために、次に簡単な電磁気学について考えてみよう。
電気力線
電界や磁界は、それぞれ、電気力線や磁力線によってイメージ化すると理解しやすい。真空中の点電荷からは、その電気量Q に比例する本数の電気力線が出ていると考えることができる。もし、真空中にただ一つの正の点電荷だけが存在しているとすれば、電気力線は点電荷から四方八方に等方的に広がり、電気力線が途中で生じることも消滅することもなく、すべての力線は無限遠方に達する。もし、Q が負であれば、電気力線は逆向きとなり、無限遠方から出た力線が負電荷に吸い込まれることになる。
電気力線の密度がそこでの電界の強さであり、力線の方向がそこの電界の向きであるから、点電界が作る電界の強さは点電荷の電気量に比例し、点電荷からの距離の2乗に反比例することが分かる。これは電荷を光源になぞらえて考えると分りやすい。一つの点光源があるとき、光線に垂直な面の明るさは光源の強さに比例し、光源からの距離の2乗に反比例するが、光線を電気力線と置き換えて考えれば、点電荷のつくる電界の強さも容易に理解できよう。
複数の点電荷が存在する場合には、それぞれの点電荷が作る電界をベクトル的に足し合わせればよいが、その場合にも電気力線の考えは有用である。今度は、電気力線は直線とはならず、正の電荷から出て負の電荷に吸収される。正電荷と負電荷が等量存在するとき、正電荷から出た電気力線はすべて負電荷に吸収されるが、全体の電気量の和がゼロでなければ、その分の電気量に相当する力線の他端は無限遠に達する。電気力線の端点には必ず電荷が存在し、電荷が存在しない場所で電気力線が途切れることはない。
電界のなかに、新たに一つの点電荷を置くと、その点電荷には、点電荷の電気量とその場所での電界の強さに比例した力が働く。二つの点電荷が存在するとき、両者の間に働く力は、一方の点電荷が作る電界によって他方の電荷が力を受けると考えればよい。これから二つの点電荷の間に働く力は、両者の電気量の積に比例し、両者の間の距離の二乗に反比例し、力の向きは両者の電気量が同符号なら斥力、異符号なら引力となる。
二つの電荷のうち、一方が電界を作り、その電界のなかで他方の電荷が力を受けると考えてクーロン力を説明したが、次に見方を変えて、二つの両方の点電荷がつくる電気力線の様子からクーロン力を考えてみよう。
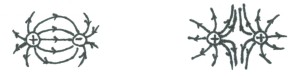
例えば、電気量の絶対値が等しい正と負の電荷があると、電気力線は図3の左図のように、正電荷から出て負電荷に吸い込まれる。つまり、電気力線は二つの正負の電荷を繋ぐことになるが、電気力線はゴム紐のように縮もうとする性質があり、力線どうしの間には反発力が存在すると考えよう。そうすれば、二つの電荷を繋ぐ力線が縮もうとするため、二つの電荷の間には引力が働くことが直感的に理解できよう。
また、図3の右図のように、二つの正の電荷のみが存在するときは、電気力線の吸収口が存在しないので、二つの電荷から出た電気力線は無限遠方まで伸びていくことになる。この場合、電気力線が互いに反発することを考えれば、ともに正の電気量を持つ電荷の間には斥力が働くことも図から直感的に理解できよう。ともに負の電荷をもつ二つの電荷の場合には③の電気力線の向きが逆になるだけであり、やはり力線どうしの反発力により斥力となる。
磁力線
磁石にはN極とS極が存在し、N極から出た磁力線がS極に吸い込まれている。磁力線の向きが磁界の向きでもある。磁力線にも、電気力線と同じく縮もうとする張力と、磁力線どうしの反発力があると考えると、磁気的な力も容易にイメージ化することができる。
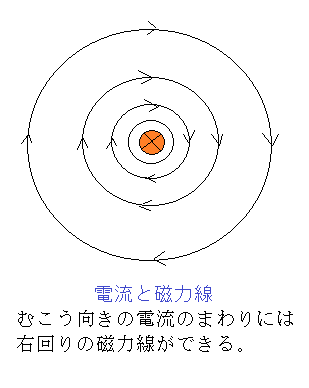
磁力線は磁石によってだけでなく直線電流によってもつくられる。図4のように手前から向こうに電流を流すと、電流の周りには同心円状に右回りの磁力線が作られる。これはアンペールの定理と呼ばれ、それは電流の近くに磁針を近づけることによって確かめられる。つまり、手前から向こうへ流れる電流の上に磁針を置くと、磁針のN極は右を向き、電流の下に磁針を置くとN極は左を向く。
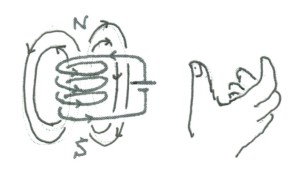
それでは、導線をコイルにして、電流を流したら、どのような磁力線ができるだろうか。それは図4をもとにして考えれば、コイルの周りには図5のような磁力線ができて、コイルは電磁石になることが理解できよう。電磁石のNSは、図5のように、右手を出して、親指以外をコイルに流れる電流の向きに合わせれば、親指の向きがN極であるが、そうなることは、コイルに流れる電流のまわりにできる磁力線の向きからも分かろう。この場合、コイルの内側では磁力線の密度が外側より大きくなるので、その反発力によって、コイルには、その径を押し広げようとする力が働く。一方、磁力線は縮もうともするので、コイルには、その長さ方向にコイルを押し潰すような力が働くことも分かる。これはマックスウェルの応力と呼ばれ、大電流が流れる電磁石を設計する場合には重要となる。
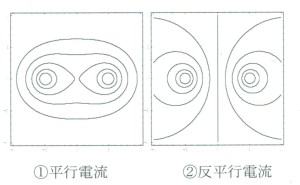
次に、二本の平行な導線に直線電流が流れている場合を考えてみよう。この場合、二本の電流が作る磁界はそれぞれの電流が作る磁界の重ね合わせとなる。図6の①のように、二本の平行電流が同じ向きなら、重ね合わせた磁界は電流と電流の間では打ち消しあって弱くなり、外側では強めあうため、重ねあわされた磁界の磁力線の密度は①のように電流の間で疎になり、外で密となり、二つの電流を取り囲む閉じた磁力線が存在する。そのため、輪ゴムで括られた二本の棒のように同方向の電流には引力が働くことになる。一方、図6の②のように、二つの電流の向きが互いに逆向きの場合、二つの電流の間で磁界は強めあい、外側では逆向きとなり弱めあうので、磁力線の様子は②のようになる。磁力線の反発力によって、逆向きの二つの電流の間には斥力が働くことがわかる。
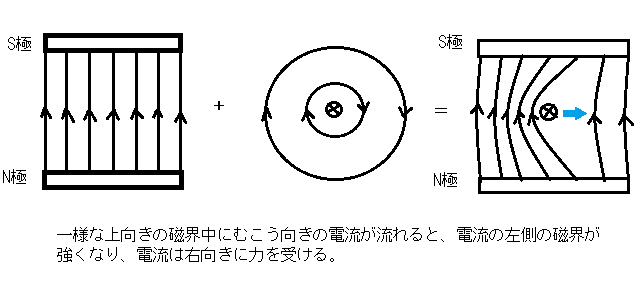
次に、図7のように、一様な磁界の中を流れる電流が受ける力を考えてみよう。上向きの一様な磁界中を電流が向こう向きに流れているとき、外部磁界(左図)と電流が作る磁界(中図)とを重ね合わせると、両者の合成磁界(右図)は電流の左側では強めあい、右側では弱めあうので、重ね合わせた磁界の磁力線の様子をイメージすることができる。磁力線の張力と反発力から、電流には右向きの力が働くことが理解できよう。これはフレミングの左手の法則と一致することがわかる。このように、磁力線の張力と磁力線どうしに働く反発力を考えることによって、磁界のなかに置かれた電流の受ける力や電流同士に働く力をイメージ化することができる。
ローレンツ力
磁界のなかを流れる電流はフレミングの左手の法則に従い、磁界から力を受けるが、これは導線の中を運動する荷電粒子が磁界から力を受けるためである。一様な磁界の中に、磁界の向きと垂直に電荷 を持った荷電粒子をある速度で入射させると、その後、荷電粒子は磁界から力を受け、サイクロトロン運動と呼ばれる円運動をする。円運動をするからには、荷電粒子は中心方向の力を受けているはずであるから、その力は磁界の向きに垂直で、荷電粒子の速度の向きにも垂直である。磁界のなかを運動する荷電粒子が受けるこの力をローレンツ力という。荷電粒子の電荷の符号がが正の場合、左手の人差し指を磁界の向き、中指を電荷の運動の向きに合わせれば、ローレンツ力は親指の向きに働くことになる。負電荷の場合にはそれと逆向きになる。
モーター
モーターは、界磁とその中をまわる回転子のコイル、それに一対のブラシからなっている。電流は電源の正極からブラシを経て回転子の中を流れ、もう一つのブラシを経て、電源の負極へ流れる。モーターがまわるしくみについては二つの説明方法があろう。一つは磁界のなかの電流が受ける力による説明方法であり、もう一つは、電磁石になった回転子と、固定磁石の間の相互作用として考える方法である。
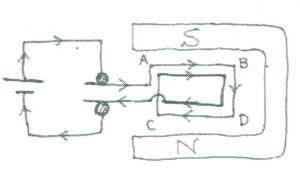
今、モーターの回転子が図8のようになっている瞬間を考えてみよう。第一の説明方法では、回転子のABの部分は、この瞬間、上向きの磁界のなかを電流が右に向かって流れているから、フレミングの左手の法則から、手前向きの力が働く。一方CDの部分では、磁界は同じ向きで変わらないが、電流の向きはABの部分とは逆向きであるので、向こう向きの力が働く。そのため、回転子に回転モーメントが働き回転する。図の状態から回転子が1/4回転すると、ブラシによって、電流の向きが切り替わる。そして半回転後はABとCDの配置が図の状態と入れ替わるが、コイルの上部になったCDには手前向きの力が働き、下部になったABには向こう向きの力が働くので、回転子は同じ向きにまわり続ける。
回転子が電磁石になることから、第二の説明方法が可能となる。図8の状態では、電流がABDCの向きに流れているから、回転子の向こう側がN極、手前側がS極になる。それぞれの極は固定磁石のN極とS極から、引力と反発力を受けて、回転子が回転する。その後は、前述のように、ブラシによって電流の流れの向きが切り替えられ、モーターは同じ向きに回り続ける。
モーターを電池から切り離し、回転子を外力によって回転させると直流発電機になる。図の回転子のABの部分やCDの部分が、固定磁石による磁界の中を、磁力線を横切って運動するので、フレミングの右手の法則に従って、起電力が生じるのである。しかし、これを右手の法則でなく、ローレンツ力、つまり、モーターと同じ左手の法則から説明することもできる。それを、次に試みてみよう。
磁場中を運動する導体
発電機の場合の起電力が生じるしくみを考えるために、図のように、下から上に向かう磁界の中で金属片を手前から向こうに動かしてみよう。金属片のなかの正電荷も金属片と一緒に向こう向きに運動するから、磁界からローレンツ力を受け、正電荷は金属片のなかを右向きに移動しようとする。一方、金属片のなかの負電荷は、正電荷と逆向きのローレンツ力を受けるので、金属片のなかを左に動こうとする。つまり金属片には右向きの起電力が生じる。これが発電機の原理である。
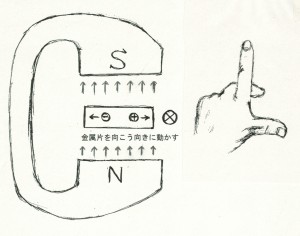
発電機の原理はローレンツ力、あるいはそれと等価なフレミングの左手の法則から説明できたが、今度は右手を出して、磁力線の向き(上向き)に人差し指をあわせ、導体を動かす向き(向こう向き)に親指を合わせると、中指の向きに電流を流そうと起電力が生じることになる。これが発電機の原理を表すフレミングの「右手」の法則である。フレミングの「左手」の法則と「右手」の法則は独立の法則ではなく、モーターの原理も発電機の原理も、そのもとを辿れば、磁界中の電流が受ける力、さらにもとを辿れば磁界中を運動する電荷に働くローレンツ力によるものである。
おわりに
一見、複雑そうに思えるモーターや発電機の仕組みだが、図4を知っていれば、電流間に働く力、図6が理解でき、モーターや発電機の仕組みがわかり、カーボンニュートラル時代のエコカーとして期待される電気自動車EVの原理が容易に理解できよう。

コメント
フレミング右手左手の法則をあてはめ、それぞれモーター 発電機に適応すると力の働く向きが同じ方向になるってことですか?
電気自動車やハイブリッドカーのモーターは坂道を下るときは発電機の役目をしてバッテリーを充電し、坂道を登るときはバッテリーの電力を使ってモーター本来の役目をしますが、回転の向きはどちらも同じです。それは、発電機の場合はフレミングの右手の法則、モーターの場合は左手の法則を使えば、説明できますが、両方のどちらの場合にも左手の法則を使っても説明できるということです。